In this problem an object is pulled along a ramp but the object starts and ends at rest and thus has no overall change in its kinetic energy ( that is important). Figure 8-10a shows the situation. A rope pulls a 200 kg sleigh ( which you may know) up a slope at incline angle $θ = 30^{\circ}$ , through distance $d = 20$ m. The sleigh and its contents have a total mass of 200 kg. the snowy slope is so slippery that we take it to be frictionless. How much work is done by each force acting on the sleigh ?

Text Solution

Verified by Experts

KEY IDEAS
(1) During the motion, the forces are constant in magnitude and direction and thus we can calculate the work done by each with Eq. 8-7 $(W = F d cos ϕ)$ in which $ϕ$ is the angle between the force and the displacement. We reach the same result with Eq. 8-8 $(W = \to F \cdot \to d)$ in which we take a dot product of the force vector and displacement vector. (2) We can relate the net work done by the forces to the change in kinetic energy energy ( or lack of a change, as here) with the work-kinetic energy theorem of Eq. 8-10 $(Δ K = W)$ .
Calculations: The first thing to do with most physics problems involving forces is to draw a free-body diagram to organize our thoughts. For the sleigh, Fig, 8-10b is our free-body diagram, showing the gravitational force ${\to F}_{g}$ , the force $\to T$ from the rope, and the normal force ${\to F}_{N}$ from the slope.
Work $W_{N}$ by the normal force, Let.s start with this easy calculation. The normal force is perpendicular to the

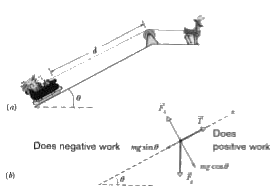
Figure 8-10 (a) A sleigh is pulled up a snowy slope. (b) The freebody diagram for the sleigh.
slope and thus also to the sleigh.s displacement. Thus the normal force does not affect the sleigh.s motion and does zero work. To be more formal, we can apply Eq. 8-7 to write
$W_{N} = F_{N} d {cos 90}^{\circ} = 0$ .
Work $W_{g}$ by the gravitational force. We can find the work done by the gravitational force in either of two ways (you pick the more appealing way). From an earlier discussion about ramps (Sample Problem 5.06 and Fig. 5-23), we know that the component of the gravitational force along the slope has magnitude mg $sin θ$ and is directed down the slope. Thus the magnitude is
$F_{g x} = m g sin θ = (200 k g) (9.8 m / s^{2}) {sin 30}^{\circ}$
$= 980 N$ .
The angle $ϕ$ between the displacement and this force component is $180^{\circ}$ . So we can apply Eq. 8-7 to write
$W_{g} = F_{g x} d {cos 180}^{\circ} = (980 N) (20 m) (- 1)$
$= - 1.96 \times 10^{4} J$ .
The negative result means that the gravitational force removes energy from the sleigh.
The second (equivalent) way to get this result is to use the full gravitational force ${\to F}_{g}$ instead of a component. The angle between ${\to F}_{g}$ and $\to d$ is $120^{\circ}$ (add the incline angle $30^{\circ}$ to $90^{\circ}$ ). So, Eq. 8-7 gives us
$W_{g} = F_{g} d {cos 120}^{\circ} = m g d {cos 120}^{\circ}$
$= (200 k g) (9.8 m / s^{2}) (20 m) {cos 120}^{\circ}$
$= 1.96 \times 10^{4} J$ .
Work $W_{T}$ by the rope.s force. We have two ways of calculating this work. The quickest way is to use the work-kinetic energy theorem of Eq. 8-10 $(Δ K = W)$ , where the net work W done by the forces is $W_{N} + W_{g} + W_{T}$ and the change $Δ K$ in the kinetic energy is just zero (because the initial and final kinetic energies are the same-namely, zero). So, Eq. 8-10 gives us
$0 = W_{N} + W_{g} + W_{T} = 0 - 1.96 \times 10^{4} J + W_{T}$
and $W_{T} = 1.96 \times 10^{4} J$ .
Instead of doing this, we can apply Newton.s second law for motion along the $x$ axis to find the magnitude $F_{T}$ of the rope.s force. Assuming that the acceleration along the slope is zero (except for the brief starting and stopping), we can write
$F_{net. x} = m a_{x}$ ,
$F_{T} - m g {sin 30}^{\circ} = m (0)$ ,
to find
$F_{T} = m g {sin 30}^{\circ}$ .
This is the magnitude. Because the force and the displacement are both up the slope, the angle between those two vectors is zero. So, we can now write Eq. 8-7 to find the work done by the rope.s force:
$W_{T} = F_{T} d {cos 0}^{\circ} = (m g {sin 30}^{\circ}) d {cos 0}^{\circ}$
$= (200 k g) (9.8 m / s^{\circ}) ({sin 30}^{\circ}) (20 m) {cos 0}^{\circ}$
$= 1.96 \times 10^{4} J$ .

Updated on:21/07/2023

An object of 1kg mass has a momentum of 10 kg m / sec then the kinetic energy of the object will be
A100J
B50J
C1000J
D200J
An object is acted on by a retarding force of $10 N$ and at a particular instant its kinetic energy is $6 J$ . The object will come to rest after it has travelled a distance of
A $3 / 5$
B $5 / 3$
C $4 m$
D $16 m$
A lawn roller is pulled along a horizontal surface through a distance of $20 m$ by a rope with a force of $200 N$ . If the rope makes an angle of $60^{\circ}$ with the vertical while pulling, the amount of work done by pulling force is
A4000 J
B1000 J
C $2000 \sqrt{3} J$
D2000 J