An elevator cab of mass $m = 500$ kg is descending with speed $v_{i} = 4.0 m / s$ when its supporting cable begins to slip, allowing it to fall with constant acceleration $\to a = \to g / 5$ (Fig. 8-11a).
(b) During the 12 m fall, what is the work $W_{T}$ done on the cab by the upward pull $\to T$ of hte elevator cable?

Text Solution

Verified by Experts

KEY IDEA
We can calculate work $W_{T}$ with Eq. 8-7 $(W = F d cos ϕ)$ by first writing $F_{net . y} = m a_{y}$ for the components in Fig. 8-11b.
Calculations: We get
$T - F_{g} = m a$ . (8-18)
Solving for .I., substituting mg for $F_{g}$ , and then substituting the result in Eq. 8-7, we obtain
$W_{T} = T d cos ϕ = m (a + g) d cos ϕ$ . (8-19)

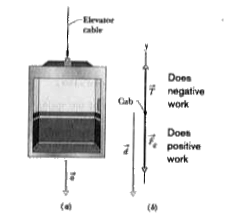
Figure 8-11 An elevator cab, descending with speed $v_{i}$ , suddenly begins to accelerate downward. (a) It moves through a displacement $\to d$ with constant acceleration $\to a = g / 5$ . (b) A freebody diagram for the cab, displacement included.
Next, substituting $- g / 5$ for the (downward) acceleration a and then $180^{\circ}$ for the angle $ϕ$ between the direction of forces $\to T$ and $m \to g$ , we find
$W_{T} = m (- \frac{g}{5} + g) d cos ϕ = \frac{4}{5} m g d cos ϕ$
$= \frac{4}{5} (500 k g) (9.8 m / s^{2}) (12 m) {cos 180}^{\circ}$
$= - 4.70 \times 10^{4} j \approx - 47 k J$ .
Caution: Note that $W_{T}$ is not simply the negative of $W_{g}$ because the cab accelerates during the fall. Thus, Eq. 8-16 (which assumes that the initial and final kinetic energies are equal) does not apply here.

Updated on:21/07/2023