An elevator platform is going up at a speed of 20m/s and during its upward motion a small ball of 50g mass, falling in downward direction, strikes the platform at speed 5m/s. Find the speed with which the ball rebounds.
To solve the problem step by step, we will use the concept of the coefficient of restitution and the principles of relative velocity in collisions.
1. Identify the Given Data:
- Mass of the ball, m=50g=0.05kg (convert grams to kilograms)
- Speed of the elevator (upward), Ve=20m/s
- Speed of the ball before collision (downward), u=5m/s
2. Define the Directions:
- Upward direction is positive.
- Downward direction is negative.
3. Determine the Velocities:
- The velocity of the ball before the collision (downward) is −u=−5m/s.
- The velocity of the elevator is Ve=20m/s.
4. Use the Coefficient of Restitution:
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- For a perfectly elastic collision, e=1.
5. Calculate the Velocity of Separation and Approach:
- Velocity of approach = Velocity of ball before collision−Velocity of elevator
Velocity of approach=−5−20=−25m/s
- Velocity of separation = Velocity of ball after collision−Velocity of elevator
Velocity of separation=v−20
6. Set Up the Equation Using Coefficient of Restitution:
- Since e=1:
1=v−20−25
7. Solve for v:
- Rearranging the equation gives:
v−20=−25
v=−25+20
v=−5m/s
8. Interpret the Result:
- The negative sign indicates that the ball is moving in the opposite direction after the collision, which means it rebounds upward.
Final Answer:
The speed with which the ball rebounds is 25m/s upward.
- Mass of the ball, m=50g=0.05kg (convert grams to kilograms)
- Speed of the elevator (upward), Ve=20m/s
- Speed of the ball before collision (downward), u=5m/s
- Upward direction is positive.
- Downward direction is negative.
- The velocity of the ball before the collision (downward) is −u=−5m/s.
- The velocity of the elevator is Ve=20m/s.
- The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- For a perfectly elastic collision, e=1.
- Velocity of approach = Velocity of ball before collision−Velocity of elevator
Velocity of approach=−5−20=−25m/s
- Velocity of separation = Velocity of ball after collision−Velocity of elevator
Velocity of separation=v−20
- Since e=1:
1=v−20−25
- Rearranging the equation gives:
v−20=−25
v=−25+20
v=−5m/s
- The negative sign indicates that the ball is moving in the opposite direction after the collision, which means it rebounds upward.
The speed with which the ball rebounds is 25m/s upward.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A ball dropped from a bridge strikes the water in 5 s. Calculate
the speed with which it strikes
View SolutionA ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View SolutionA ball of mass 2 kg is projected horizontally with a velocity 20m/s from a building of height 15m. The speed with which body hits the ground is :
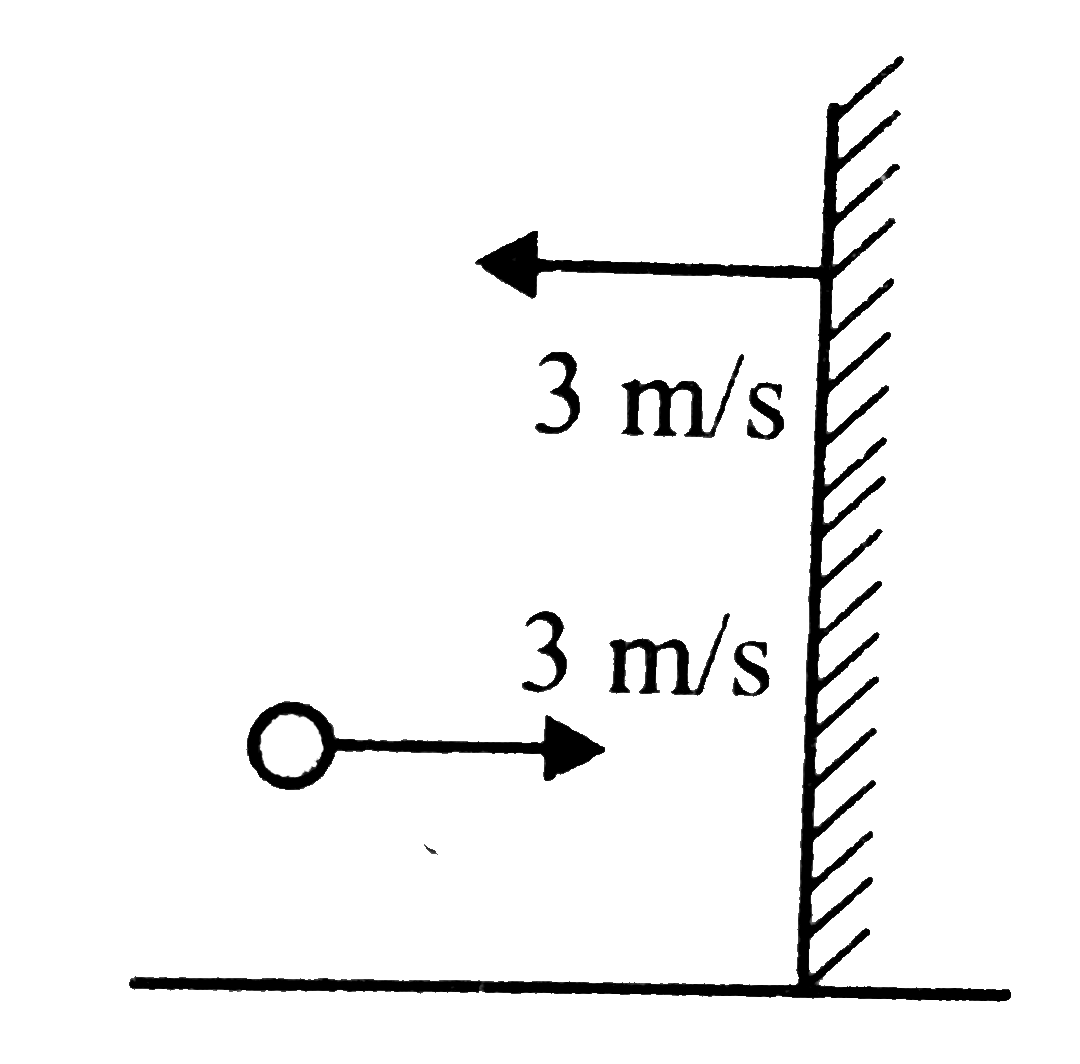
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
View SolutionA lift is moving in upward direction with speed 20m/s and having acceleration 5m/s2 in downward direction. A bolt drops from the ceiling of lift at that moment. Just after the drop, the:
View SolutionA ball moving vertically downward with a speed of 10m/s collides with a platform. The platform moves with a velocity of 5m/s in downward direction. If e=0.8, find the speed (in m/s ) of the ball just after collision.
View SolutionA metal plate of mass 200g is balanced in mid air by throwing 40 balls per second, each of mass 2g vertically upwards from below. The balls get rebounded with the same speed with which they strike the plate. Find the speed with which the balls strike the plate.
View SolutionA platform is moving upwards with a constant acceleration of 2ms−2. At time t=0, a boy standing on the platform throws a ball upwards with a relative speed of 8ms−1. At this instant, platform was at the height of 4m from the ground and was moving with a speed of 2ms−1. Take g=0ms−2. Find
(a) when and where the ball strikes the platform.
(b) the maximum height attained by the ball from the ground.
( c) the maximum distance of the ball from the platform.
View SolutionA ball falls from a height such that it strikes the floor of lift at 10 m/s. If lift is moving in the upward direction with a velocity 1 m/s, then velocity with which the ball rebounds after elastic collision will be
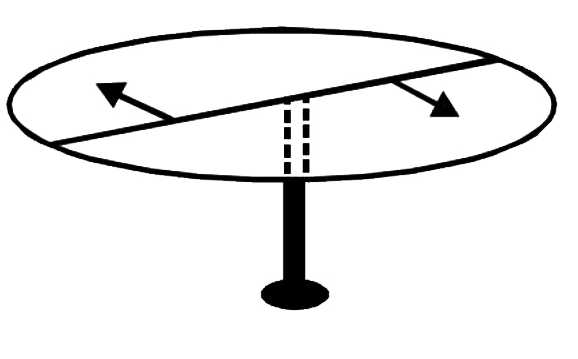
View SolutionA horizontal circular platform of radius 0.5 m and mass axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of 9ms−1 with respect to the ground. The rotational speed of the platform in rads−1 after the balls leace the platform is
View Solution
