In Fig. 8-15b, an 8.0 kg block slides along a frictionless floor as a force acts on it, starting at x1=0 and ending at x3=6.5m. As the block moves, the magnitude and direction of the force varies according to the graph shown in Fig. 8-15a. For example, from x = 0 to x = 1 m, the force is positive (in the positive direction of the x axis) and increase in magnitude from 0 to 40 N. And from x = 4 m to x = 5, the force is negative and increases in magnitude from 0 to 20 N.
(Note that this latter value is displayed as -20 N.) The block's kinetic energy at x1 is K1=280J. What is the block's speed at x1=0,x2=4.0m, and x3=6.5m ?
KEY IDEAS
(1) At any point, we can relate the speed of the block to its kinetic energy with Eq. 8-1 (K=1/2mv2). (2) We can relate the kinetic energy Kf at a later point to the initial kinetic Ki and the work W done on the block by using work-kinetic energy theorem of Eq. 8-10 (Kf−Ki=2). (3) We can calculate the workk W done by a variable force F(x) by integrating the force versus position x.Equation 8-32 tells us that
W=∫xfxif(x)dx.
We do not have a functon F(x) to carry out this integration, but we do have a graph of F(x) where we an integrate by finding the area between the plotted line
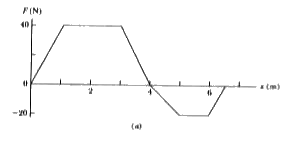
Figure 8-15 (a) A graph indicating the magnitude and direction of a variable force that acts on a block as it moves along an x axis on a floor. (b) The location of the block at several times.
and the x axis. Where the plot is obove the axis, the work (which is equal to the area) is positive. Where it is below the axis, the work is negative.
Calculations: The requested speed at x=0 is easy because we already Know the kinetic energy. So, we just plug the kinetic energy into the fromula for kinetic energy:
K1=12mv21,280J=12(8.0kg)v21,
and then
v1=8.37m/s≈8.4m/s.
As the block moves from x = 0 to x = 4.0 m, the plot in Figure 8-15a is above the x axis, which means that positive work is being done on the block. We split the area under the plot into a triangle at the left, a rectangle in the center, and a triangle at the right. Their total area is
12(40N)(1m)+(40N)(2m)+12(40N)(1m)=120N⋅m
=120J.
This means that between x = 0 and x = 4.0 m, the force does 120 J of work on the block, increasing the block reaches x = 4.0 m, the work-kinetic energy theroem tells us that the kinetic energy is
K2=K1+W=280J+120J=400J.
Again using the definition of kinetic energy, we find
K2=12mv22,400J=12(8.0kg)v22,
and then
v2=10m/s
This is the block.s greatest speed because from x = 4.0 m to x = 6.5 m the force is negative, meaning that it opposes the block.s motion, doing negative work on the block and thus decrasing the kinetic energy and speed. In that range, the area between the plot and the x axis is
12(20N)(1m)+(20N)(1m)+12(20N)(0.5m)=35N⋅m
=35J.
This means that the work done by the force in that range is -35 J. At x =4.0 m, the block .s K =400 J. At x =6.5 m,
the work-kinetic energy theroem tells us that its kinetic energy is
K3=K2+W=400J−35J=365J.
Again using the definition of kinetic, we find
K3=12mv23,365J=12(8.0kg)v33,
and then
v3=9.55m/s≈9.6m/s.
The block is still moving in the positive direction of the x axis, a bit faster than initally.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
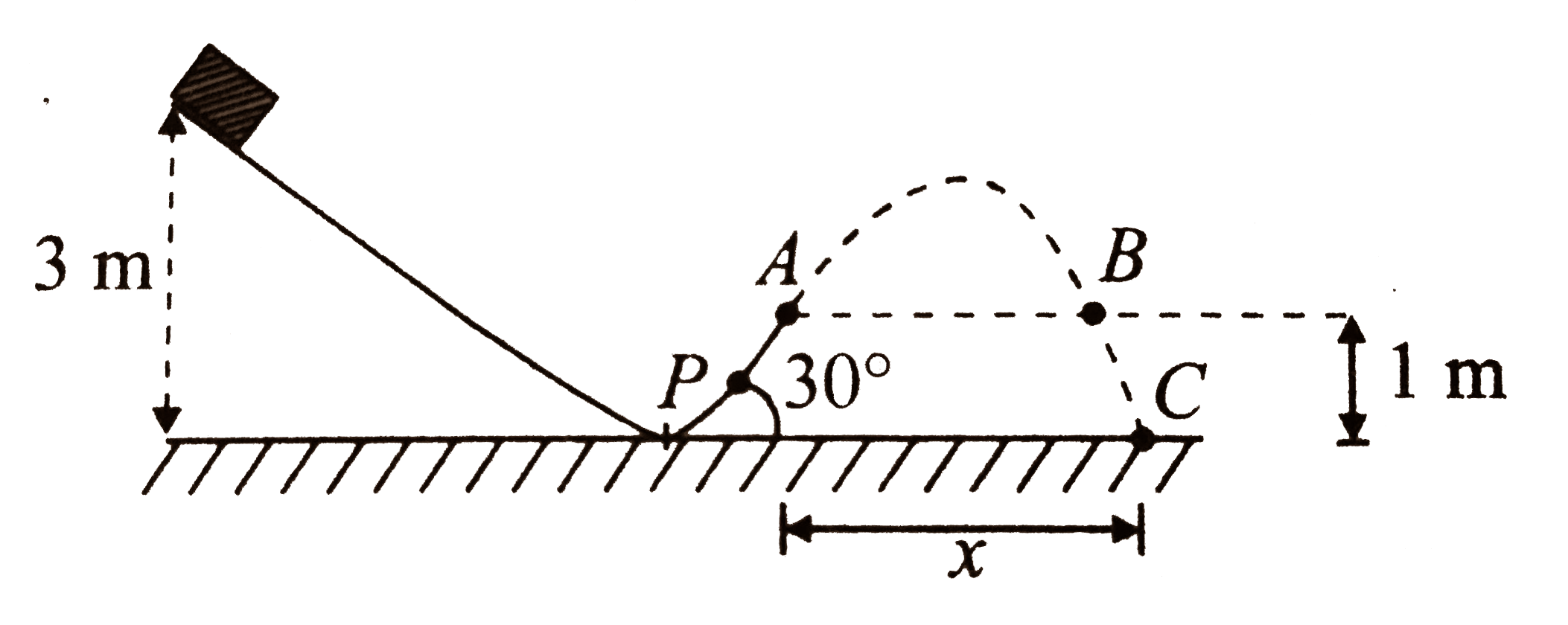 .
.
The horizontal distance x travelled by the block in moving from A to C is.
View SolutionA 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
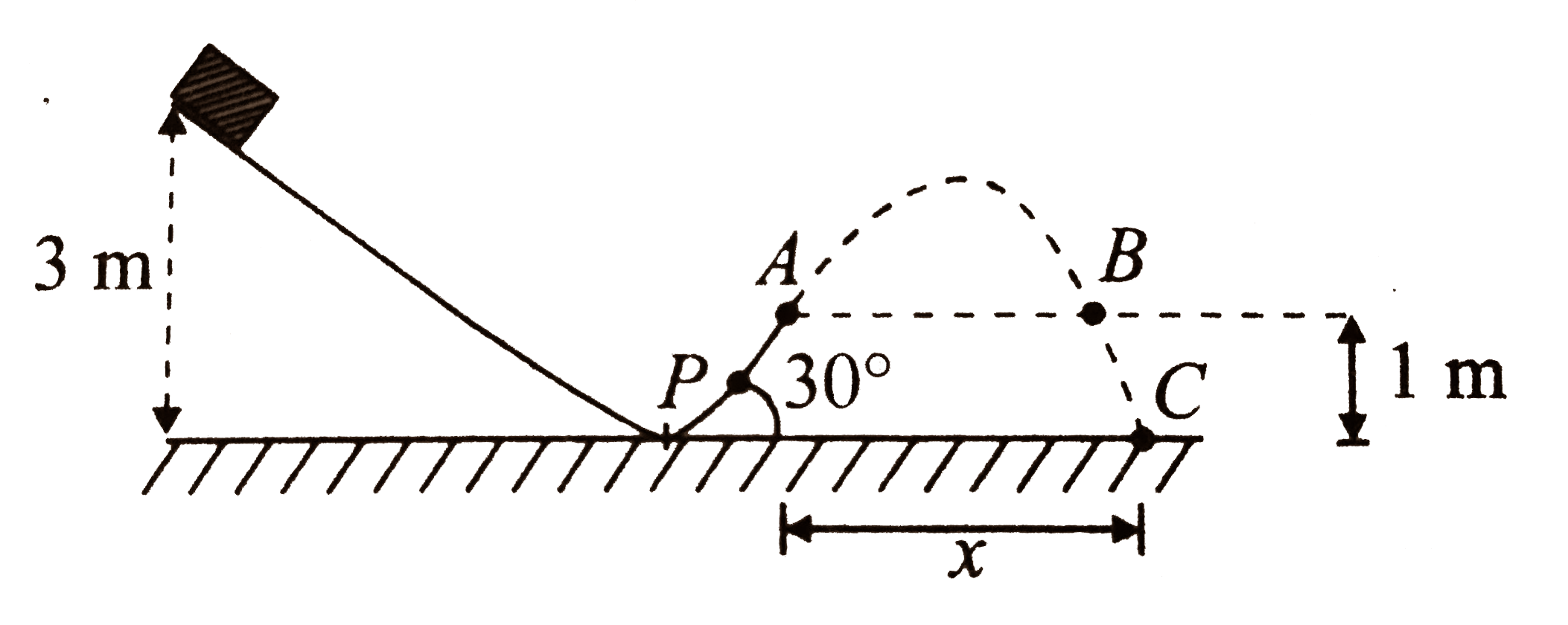 .
.
The time taken by the block to move from A to B is.
View Solution
Knowledge Check
A 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
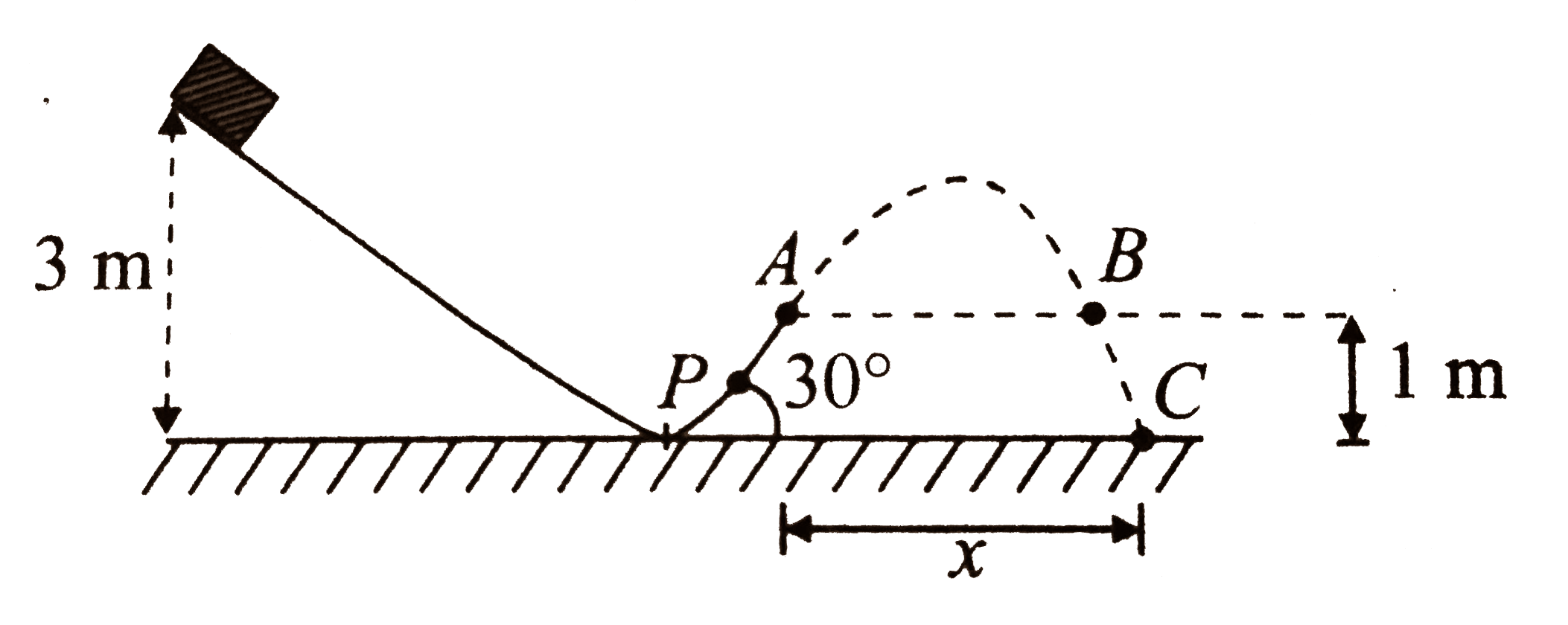 .
.
The horizontal distance x travelled by the block in moving from A to C is.A(1+√3)mB(1−√3)mC(√3+3))mDg meterA 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
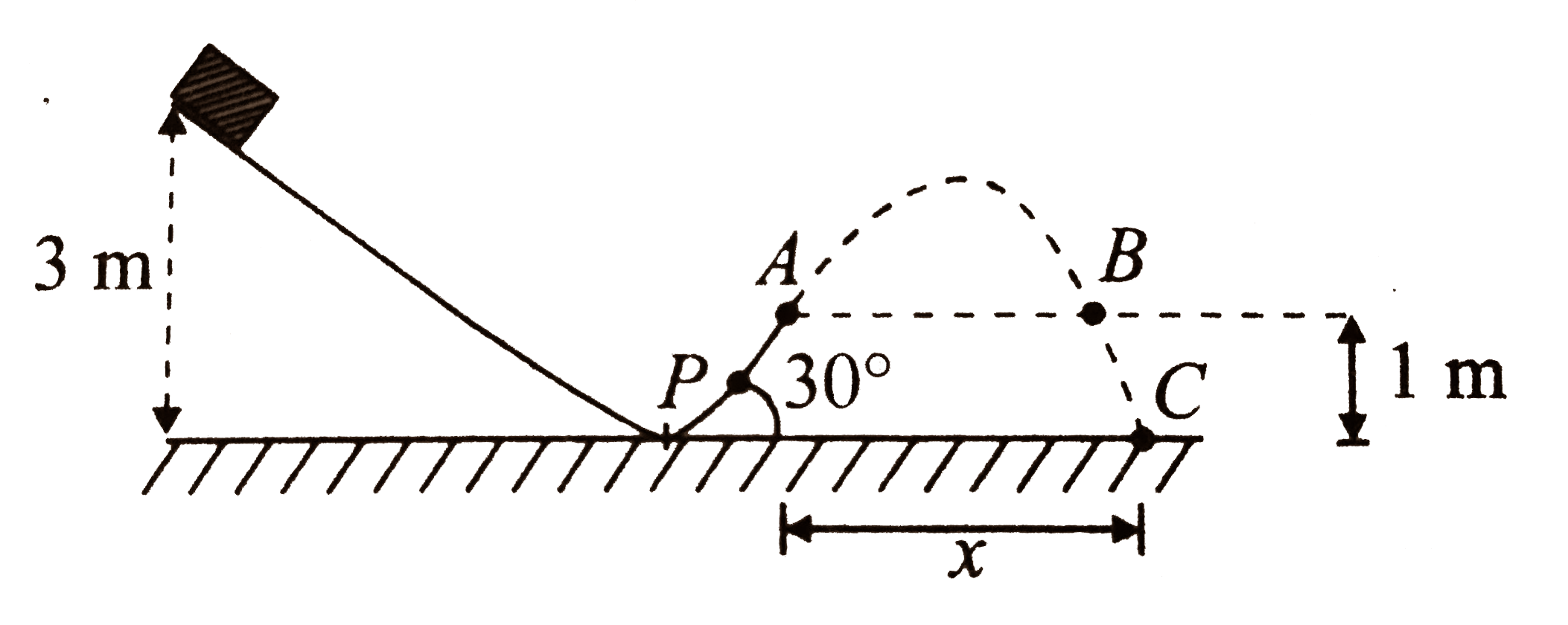 .
.
The time taken by the block to move from A to B is.A1√gB2√gC3√gD4√gA 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
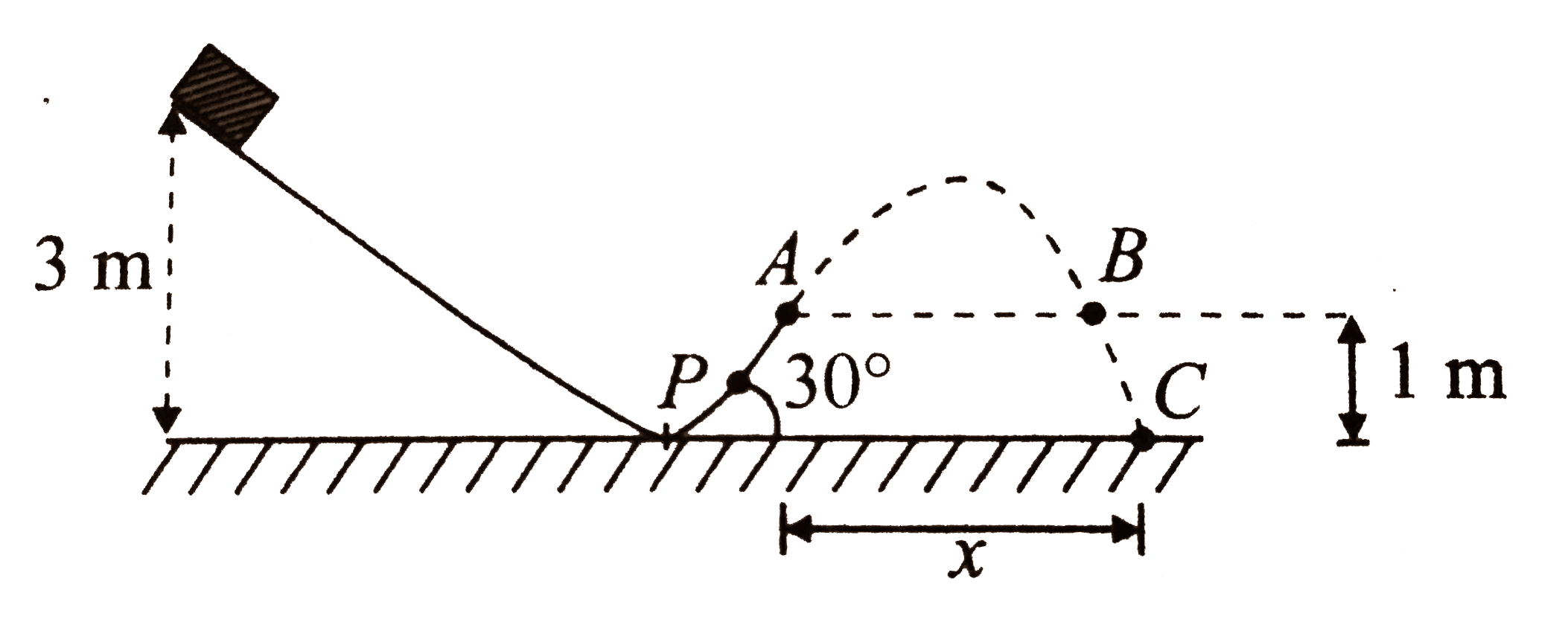 .
.
The time taken by the block to move from A to C is.A√3gB√2gC√1gD1+√3√g
A 0.098−kg block slides down a frictionless track as shown in (Fig. 5.208).
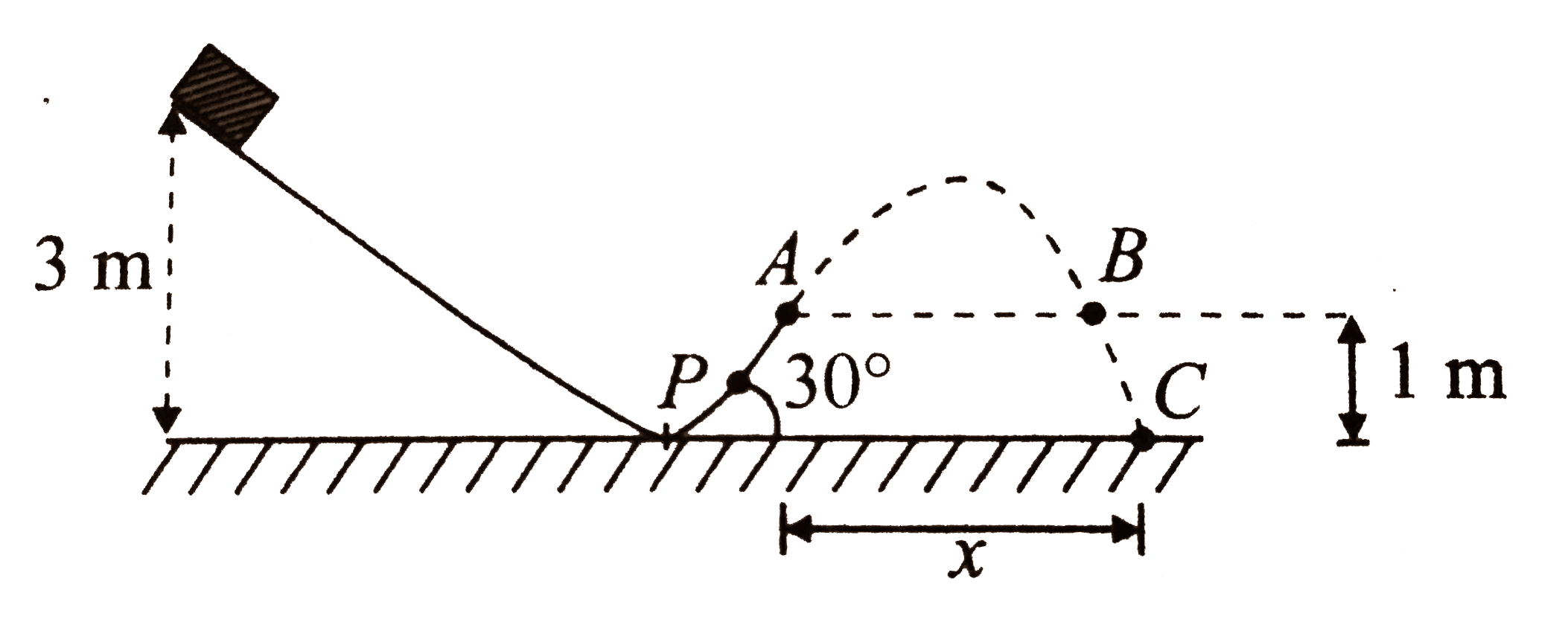 .
.
The time taken by the block to move from A to C is.
View SolutionA 10−kg block moves in a straight line under the action of a force that varies with position as shown in figure. How much work does the force do as the block moves from origin to x=8m?
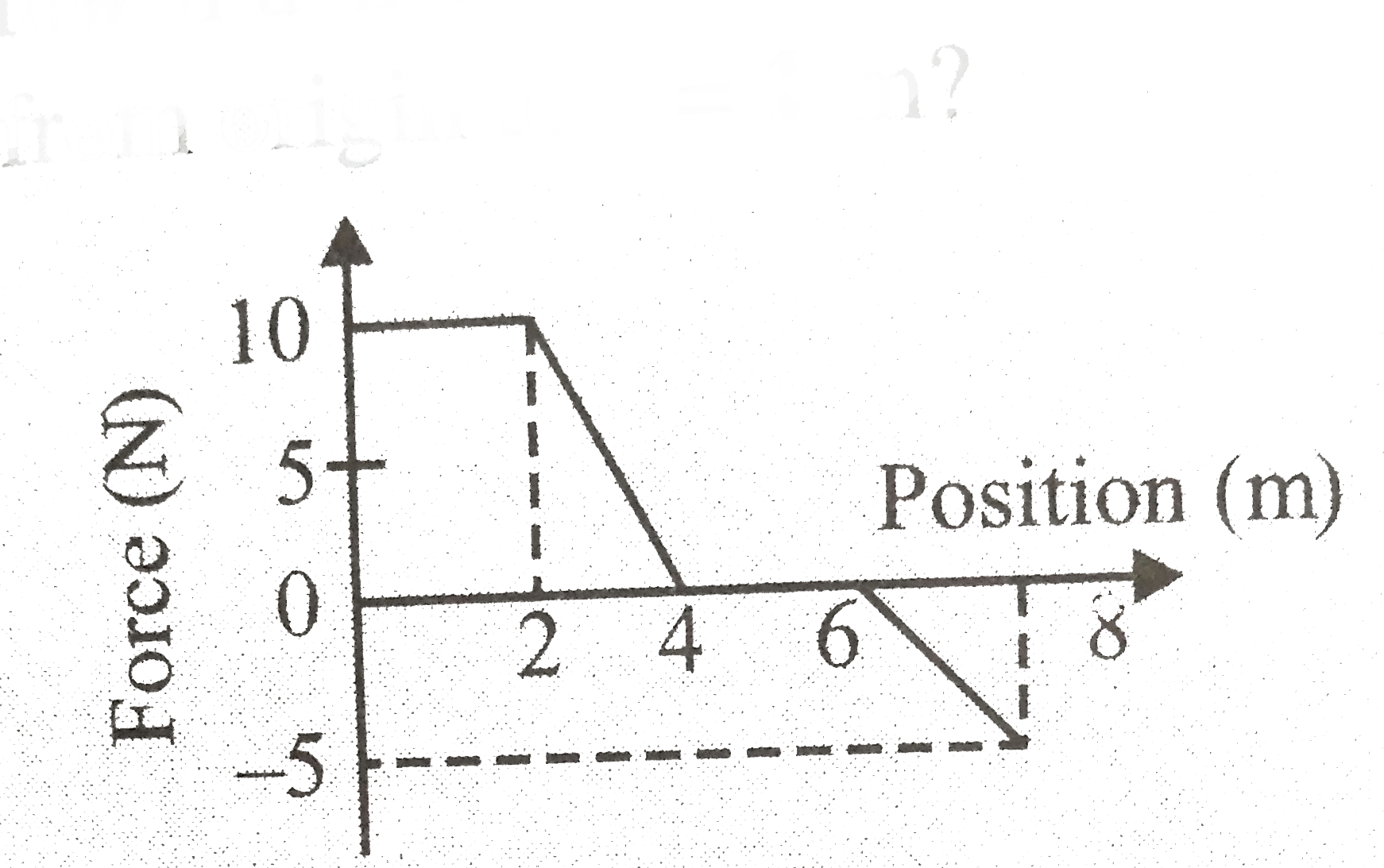
View SolutionA 10−kg block moves in a straight line under the action of a force that varies with position as shown in figure. How much work does the force do as the block moves from origin to x=8m?
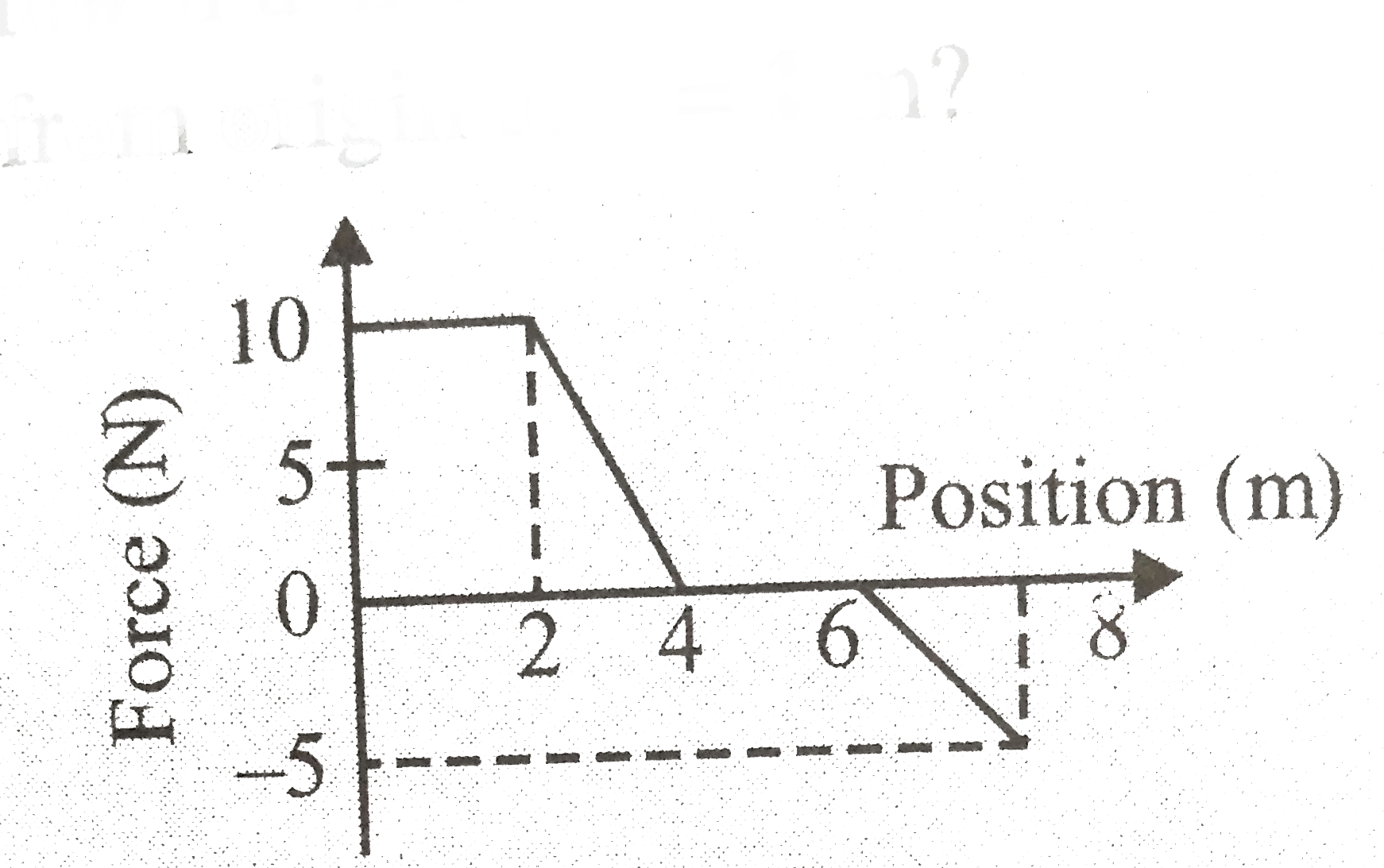
View SolutionA force F = (10+0.25x) is acting on a particle moving along positive X direction . Calculate the work done by this force during a displacement from x = 1 m to x = 4 m .
View SolutionThree components of a force acting on a particle are varying according to the graphs as shown. To reach at point B(8, 20, 0)m from point A(0, 5, 12)m the particle moves on paths parallel to x-axis then y-axis and then z-axis, then work done by this force is:
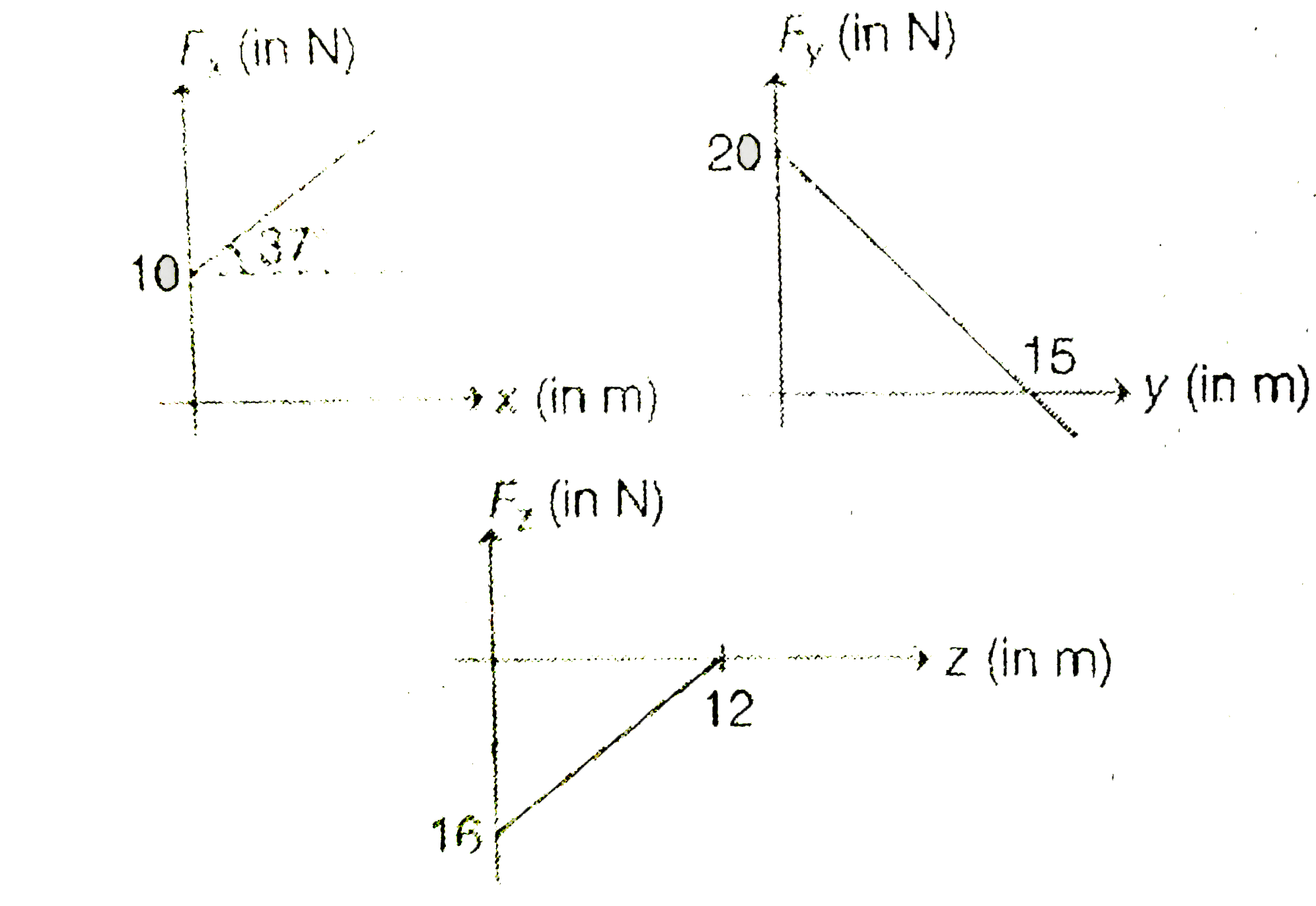
View Solution
