A 4.0 kg bundle starts up a incline with 150 J of kinetic energy. How far will it slide up the incline if the coefficient of kinetic friction between bundle and incline is 0.36 ?
The correct Answer is:4.7 m
To solve the problem, we will use the work-energy principle, which states that the work done by all forces acting on an object is equal to the change in its kinetic energy.
1. Identify the Given Data:
- Mass of the bundle, m=4.0kg
- Initial kinetic energy, KEi=150J
- Angle of incline, θ=30∘
- Coefficient of kinetic friction, μ=0.36
- Acceleration due to gravity, g=10m/s2 (approximate value)
2. Calculate the Forces Acting on the Bundle:
- The gravitational force acting down the incline:
Fgravity=mgsin(θ)=4.0×10×sin(30∘)=4.0×10×12=20N
- The normal force acting on the bundle:
Fnormal=mgcos(θ)=4.0×10×cos(30∘)=4.0×10×√32=20√3N
- The frictional force acting down the incline:
Ffriction=μFnormal=0.36×20√3≈12.47N
3. Calculate the Total Work Done Against Gravity and Friction:
- The total force acting down the incline is the sum of the gravitational force and the frictional force:
Ftotal=Fgravity+Ffriction=20+12.47=32.47N
- The work done against these forces as the bundle moves a distance s up the incline is given by:
W=Ftotal⋅s
4. Apply the Work-Energy Principle:
- The work done is equal to the change in kinetic energy:
W=KEf−KEi
- Since the final kinetic energy KEf=0 (the bundle comes to rest), we have:
−W=KEi⟹−Ftotal⋅s=−150
- Thus,
Ftotal⋅s=150
5. Solve for Distance s:
- Rearranging the equation gives:
s=150Ftotal=15032.47≈4.63m
Final Answer:
The bundle will slide up the incline approximately 4.63 meters before coming to rest.
- Mass of the bundle, m=4.0kg
- Initial kinetic energy, KEi=150J
- Angle of incline, θ=30∘
- Coefficient of kinetic friction, μ=0.36
- Acceleration due to gravity, g=10m/s2 (approximate value)
- The gravitational force acting down the incline:
Fgravity=mgsin(θ)=4.0×10×sin(30∘)=4.0×10×12=20N
- The normal force acting on the bundle:
Fnormal=mgcos(θ)=4.0×10×cos(30∘)=4.0×10×√32=20√3N
- The frictional force acting down the incline:
Ffriction=μFnormal=0.36×20√3≈12.47N
- The total force acting down the incline is the sum of the gravitational force and the frictional force:
Ftotal=Fgravity+Ffriction=20+12.47=32.47N
- The work done against these forces as the bundle moves a distance s up the incline is given by:
W=Ftotal⋅s
- The work done is equal to the change in kinetic energy:
W=KEf−KEi
- Since the final kinetic energy KEf=0 (the bundle comes to rest), we have:
−W=KEi⟹−Ftotal⋅s=−150
- Thus,
Ftotal⋅s=150
- Rearranging the equation gives:
s=150Ftotal=15032.47≈4.63m
The bundle will slide up the incline approximately 4.63 meters before coming to rest.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)59videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)10videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT6videos
WORK, POWER, AND ENERGY
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)4videos
WAVES-I
Similar Questions
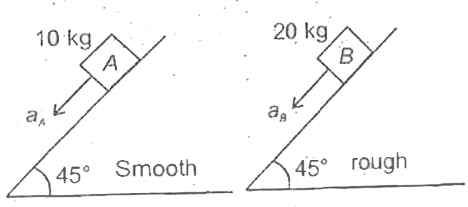
The ratio of acceleration of blocks A placed on smooth incline with block B placed on rough incline is 2:1. The coefficient of kinetic friction between block B and incline isView SolutionA piece of ics slides down a 45∘ incline in twice the time it takes to slide down a frictionless 45∘ incline . What is the coefficient of friction between the ice and the incline ? .
View Solution
Knowledge Check
- Question 1 - Select One
A given object taken double time to slide down a 45∘ rough incline as it takes to slide down a perfectly smooth 45∘ incline. The coefficient of kinetic friction between the object and the incline is given by
A14B12C34D1√2 - Question 2 - Select One
A given object takes n times as much time to slide down a 45∘ rough incline as it takes to slide down a perfectly smooth 45∘ incline. The coefficeint of kinetic friction between the object and the incline is given by:
A(1−1n2)B(11−n2)C√(1−1n2)D√(11−n2) - Question 3 - Select One
A given object taken n time more time to slide down 45∘ rough inclined plane as it taken to slide down a perfectly smooth 45∘ incline The coefficient of kintic friction between the object and the incline is .
A12−n2B1−1n2C√1−1n2D√11−n2
A block slides down an incline of angle 30∘ with an acceleration of g/4 Find the coefficient of kinetic friction .
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
 View Solution
View SolutionThe time taken by a body to slide down a rough 45∘ inclined plane is twice that required to slide down a smooth 45∘ inclined plane. The coefficient of kinetic friction between the object and rough plane is given by
View SolutionA piece of ice slides down a rough inclined plane at 45∘ inclination in twice the time that it takes to slide down an identical but frictionless inclined plane. What is the coefficient of friction between ice and incline ?
View SolutionA body takes n times as much time to slide down a 45∘ rough incline as it takes to slide down a smooth 45∘ incline. The coefficient of friction between the body and the incline will be
View Solution

