You push a 2.0 kg block against a horizontal spring , compressing the spring by 12 cm. Then You release the block, and the spring sends it sliding across a tabletop. It stops 75 cm from where you released it. The spring constant is 170 N/m. What is the block-table coefficient of kinetic friction ?
The correct Answer is:μk=0.083
To find the coefficient of kinetic friction (μ_k) between the block and the tabletop, we can follow these steps:
Step 1: Calculate the potential energy stored in the spring
The potential energy (PE) stored in a compressed spring can be calculated using the formula:
PE=12kx2
where:
- k=170N/m (spring constant)
- x=0.12m (compression of the spring)
Substituting the values:
PE=12×170N/m×(0.12m)2
PE=12×170×0.0144
PE=12×2.448J
PE=1.224J
Step 2: Calculate the work done by friction
The work done by friction (W_f) can be expressed as:
Wf=Ff×d
where:
- Ff=μk×m×g (frictional force)
- d=0.75m (distance the block slides)
Substituting the expression for frictional force:
Wf=μk×m×g×d
where:
- m=2kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
So,
Wf=μk×2kg×10m/s2×0.75m
Wf=μk×15N
Step 3: Set the work done by friction equal to the potential energy
Since all the potential energy from the spring is converted into work done against friction, we can set them equal:
μk×15=1.224
Step 4: Solve for μ_k
Now, we can solve for the coefficient of kinetic friction (μ_k):
μk=1.22415
μk=0.0816
Final Answer
The coefficient of kinetic friction (μ_k) between the block and the tabletop is approximately:
μk≈0.08
---
The potential energy (PE) stored in a compressed spring can be calculated using the formula:
PE=12kx2
where:
- k=170N/m (spring constant)
- x=0.12m (compression of the spring)
PE=12×170N/m×(0.12m)2
PE=12×170×0.0144
PE=12×2.448J
PE=1.224J
The work done by friction (W_f) can be expressed as:
Wf=Ff×d
where:
- Ff=μk×m×g (frictional force)
- d=0.75m (distance the block slides)
Wf=μk×m×g×d
where:
- m=2kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
Wf=μk×2kg×10m/s2×0.75m
Wf=μk×15N
Since all the potential energy from the spring is converted into work done against friction, we can set them equal:
μk×15=1.224
Now, we can solve for the coefficient of kinetic friction (μ_k):
μk=1.22415
μk=0.0816
The coefficient of kinetic friction (μ_k) between the block and the tabletop is approximately:
μk≈0.08
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
59 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions

A block of mass m is pressed against a horizontal spring fixed at one end to compress the spring through (L0)/(2). The natural length of the spring is L0 and spring constant k=(mg)/(L0). When released, the block moves horizontally on smooth surface till it leaves the spring. At what horizontal distance from O it strikes the ground.
View SolutionA 700 g block is released from rest at height h0 above a vertical spring with spring constant k=450N/m and negligible mass. The block sticks to the spring and momentarily stops after compressing the spring 19.0 cm. How much work is done (a) by the block on the spring and (b) by the spring on the block ? (c) What is the value of h0 ? (d) If the block were released from height 2.00h0 above the spring, what would be the maximum compression of the spring ?
View Solution
Knowledge Check
A block with mass 0.50kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20m (figure). When released, the block moves on a horizontal table top for 1.00N/m. What is the coefficient of kinetic friction μk, between the block and the block and the table?
 A0.40B0.50C0.25Dnone of these
A0.40B0.50C0.25Dnone of theseA 2kg block slides on a horizontal floor with the a speed of 4m/s it strikes a uncompressed spring , and compresses it till the block is motionless . The kinetic friction force is compresses is 15N and spring constant is 10000N/m . The spring by
A8.5cmB5.5cmC2.5cmD11.0cmA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1
A small block of mass 500 gm is pressed against a horizontal spring fixed at one end to a distance of 10 cm. when released, the block moves horizontally till it leaves the spring. Where it will hit the ground 5 m below the spring. (Take k = 100 N/m of spring)
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View SolutionA block of mass m = 1 kg is kept pressed against a spring on a rough horizontal surface. The spring is compressed by 10 cm from its natural length and to keep the block at rest in this position a horizontal force (F) towards left is applied. It was found that the block can be kept at rest if 8N≤F≤18N. Find the spring constant (k) and the coefficient of friction (μ) between the block and the horizontal surface.
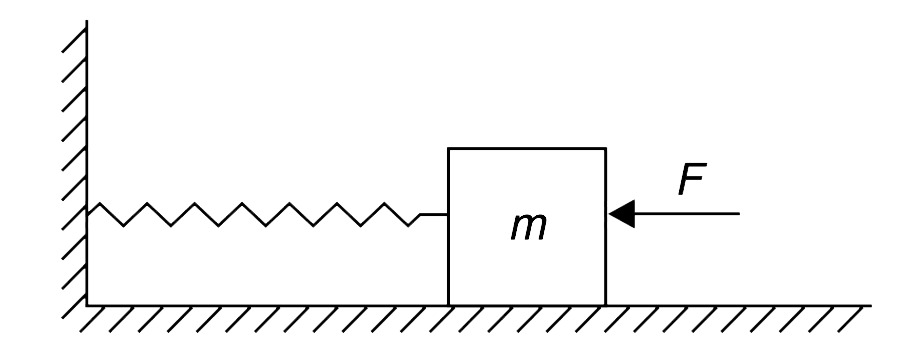
View SolutionA 2 kg block slides on a horizontal floor with a speed of 4 m/s. It strikes an uncompressed spring, and compresses it till the block is motionless. The kinetic friction force is 15 N and spring constant is 10000 N/m. The spring is compressed by (in cm):
View Solution
