Two balls of equal size are dropped from the same height from the roof of a building . One ball has twice the mass of the other. When the balls the ground, how do the kinetic energies of the two balls compare ?
The lighter one has one fourt has much kinetic energy as the other does.
The lighter one has one half as much kinetic energy as the other does.
The lighter one has the same kinetic energy as the other does.
The lighter one has twice as much kinetic energy as the other does.
The correct Answer is:B
To solve the problem, we will analyze the kinetic energies of the two balls when they reach the ground after being dropped from the same height.
1. Identify the Masses of the Balls:
- Let the mass of the lighter ball be m.
- The mass of the heavier ball is given as twice that of the lighter ball, so it is 2m.
2. Understand the Initial Conditions:
- Both balls are dropped from the same height h.
- Initially, both balls have zero kinetic energy since they are at rest.
3. Calculate Potential Energy at the Height:
- The potential energy (PE) of the lighter ball at height h is given by:
PE1=mgh
- The potential energy of the heavier ball at height h is:
PE2=2mgh
4. Use Conservation of Energy:
- According to the conservation of energy, the total mechanical energy (potential + kinetic) remains constant if we ignore air resistance.
- When the balls reach the ground, all potential energy is converted into kinetic energy (KE).
5. Calculate Kinetic Energy at the Ground:
- For the lighter ball:
KE1=PE1=mgh
- For the heavier ball:
KE2=PE2=2mgh
6. Compare the Kinetic Energies:
- Now we compare the kinetic energies:
KE1=mghandKE2=2mgh
- From this, we can see that:
KE2=2×KE1
- This means the kinetic energy of the heavier ball is twice that of the lighter ball.
7. Conclusion:
- The lighter ball has half the kinetic energy of the heavier ball when they reach the ground.
Final Answer:
The lighter ball has half as much kinetic energy as the heavier ball.
- Let the mass of the lighter ball be m.
- The mass of the heavier ball is given as twice that of the lighter ball, so it is 2m.
- Both balls are dropped from the same height h.
- Initially, both balls have zero kinetic energy since they are at rest.
- The potential energy (PE) of the lighter ball at height h is given by:
PE1=mgh
- The potential energy of the heavier ball at height h is:
PE2=2mgh
- According to the conservation of energy, the total mechanical energy (potential + kinetic) remains constant if we ignore air resistance.
- When the balls reach the ground, all potential energy is converted into kinetic energy (KE).
- For the lighter ball:
KE1=PE1=mgh
- For the heavier ball:
KE2=PE2=2mgh
- Now we compare the kinetic energies:
KE1=mghandKE2=2mgh
- From this, we can see that:
KE2=2×KE1
- This means the kinetic energy of the heavier ball is twice that of the lighter ball.
- The lighter ball has half the kinetic energy of the heavier ball when they reach the ground.
The lighter ball has half as much kinetic energy as the heavier ball.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
9 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
Two balls are dropped to the ground from different heights. One ball is dropped 2 sec after the other but they both strike the ground at the same time. If the first ball takes 5 sec to reach the ground then the diffeence in initial heights is:
View SolutionTwo balls of same mass are dropped from the same height h, on to the floor. The first ball bounces to a height h/4, after the collision & the second ball to a height h/6. The impulse applied by the first & second ball on the floor are I1 and I2 respectively. Then :-
View Solution
Knowledge Check
A ball is dropped from a height of 10 m, as it falls,
Aits velocity increases and acceleration decreases.Bits velocity decreases and acceleration increases.Cits velocity increases and acceleration remains constant.Dits velocity and acceleration remains constant.A ball released from rest from the roof of a building of height 45 m at t = 0. Find the height of ball from ground at t = 2s.
A10 mB20 mC25 mD30 mTwo balls of same mass are released simultaneously from heights h & 2h from the ground level. The balls collide with the floor & stick to it. Then the velocity-time graph of centre of mass of the two balls is best represented by :
A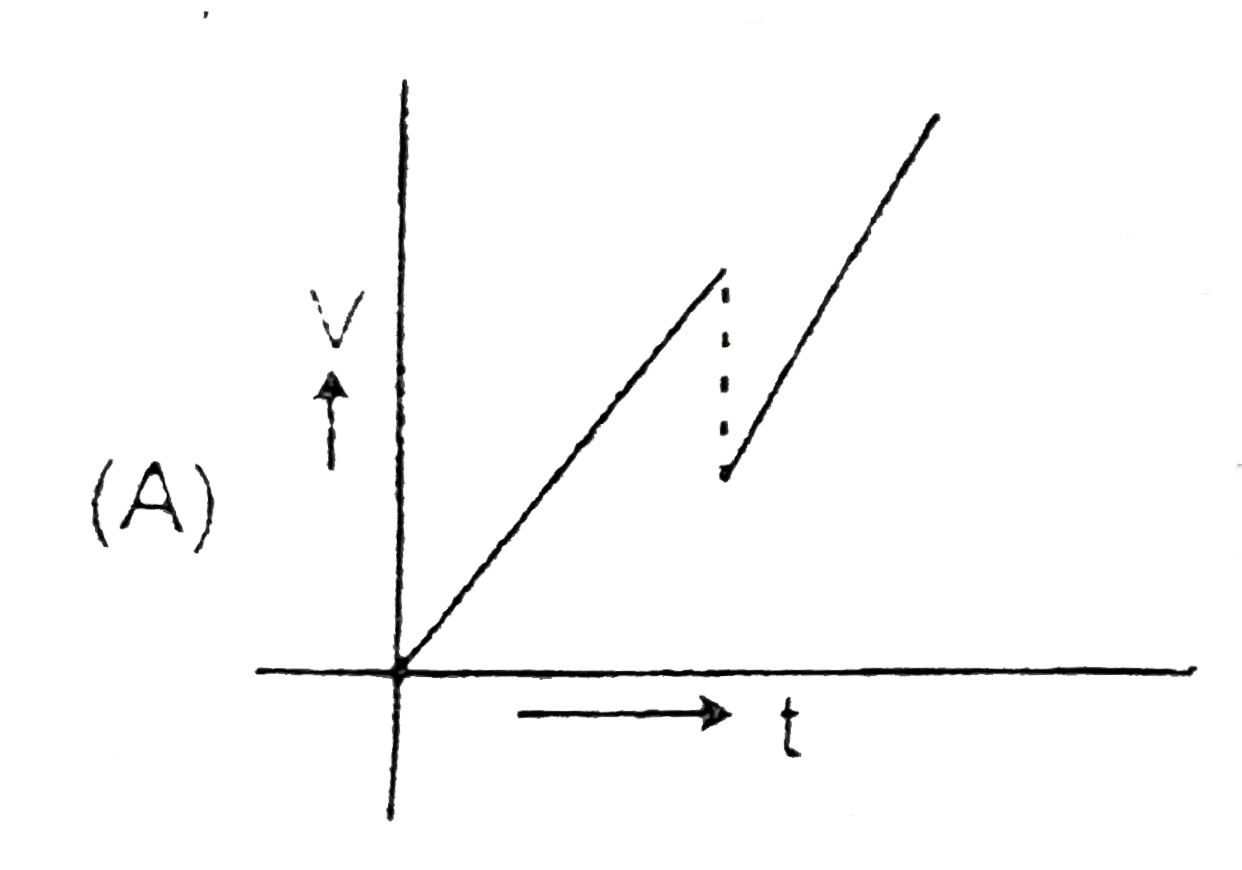 B
B C
C D
D
Two balls of same mass are dropped from the same height h, on to the floor. The first ball bounces to a height h/4, after the collision & the second ball to a height h/16. The impulse applied by the first & second ball on the floor are I1 and I2 respectively. Then
View SolutionTwo balls a A and B of same size are dropped from the same point under gravity. The mass of A is greater than that of B.If the air resistance acting on each ball is same, then
View SolutionTwo balls are dropped from heights h and 2h respectively from the earth surface. The ratio of time of these balls to reach the earth is.
View SolutionTwo balls are dropped to the ground from different heights. One ball is dropped 2 s after the other but they both strike the ground at the same time. If the first ball takes 5 s to reach the ground, then the difference in initial heights is (Take g = 10 m s−2)
View SolutionTwo balls of different masses have the same kinetic energy. Then the
View Solution
