The makes obtained by Rohit in English in his class-X final exams?
Rohit sscored 42 marks in Chemistry which was 50% of the marks that he got in Hindi which in twice as mush as mark obtained in English
II. Rohit's marks in Rnglish were 17% of the total marks he got in all the subjects together.
Data given in statement 1 alone are sufficient to answer the question whereas the data given in statement 2 alone are note sufficient to answer the question
Data given in statement 2 alone are sufficient to answer the question whereas the data given in statement 1 alone are not sifficient to answer the question.
Data in either statement 1 alone or in statement 2 alone are sufficient to answer the question.
Data in both the statement 1 and 2 not sufficient to answer the question.
The correct Answer is:A
To determine the marks obtained by Rohit in English in his class-X final exams, we will analyze the information provided in the two statements step by step.
Step 1: Analyze Statement I
Statement I: Rohit scored 42 marks in Chemistry, which was 50% of the marks that he got in Hindi, which is twice as much as the marks obtained in English.
1. Calculate marks in Hindi:
- Let the marks obtained in Hindi be H.
- According to the statement, 50% of H is equal to 42.
- This can be expressed mathematically as:
0.5H=42
- Solving for H:
H=420.5=84
2. Relate Hindi marks to English marks:
- The statement also mentions that Hindi marks are twice the marks obtained in English.
- Let the marks obtained in English be E.
- Therefore, we have:
H=2E
- Substituting the value of H:
84=2E
- Solving for E:
E=842=42
Conclusion from Statement I:
From Statement I, we find that Rohit scored 42 marks in English.
Step 2: Analyze Statement II
Statement II: Rohit's marks in English were 17% of the total marks he got in all subjects together.
1. Let the total marks in all subjects be T.
- According to the statement, we can express the marks in English as:
E=0.17T
- However, we do not have the value of T from this statement, so we cannot determine E directly.
Conclusion from Statement II:
Statement II alone is not sufficient to determine the marks obtained by Rohit in English, as we do not have the total marks T.
Final Conclusion:
Since Statement I alone is sufficient to determine the marks obtained by Rohit in English, while Statement II is not, we conclude that the answer is based solely on Statement I.
Answer:
Rohit scored 42 marks in English.
---
Statement I: Rohit scored 42 marks in Chemistry, which was 50% of the marks that he got in Hindi, which is twice as much as the marks obtained in English.
- Let the marks obtained in Hindi be H.
- According to the statement, 50% of H is equal to 42.
- This can be expressed mathematically as:
0.5H=42
- Solving for H:
H=420.5=84
- The statement also mentions that Hindi marks are twice the marks obtained in English.
- Let the marks obtained in English be E.
- Therefore, we have:
H=2E
- Substituting the value of H:
84=2E
- Solving for E:
E=842=42
From Statement I, we find that Rohit scored 42 marks in English.
Statement II: Rohit's marks in English were 17% of the total marks he got in all subjects together.
- According to the statement, we can express the marks in English as:
E=0.17T
- However, we do not have the value of T from this statement, so we cannot determine E directly.
Statement II alone is not sufficient to determine the marks obtained by Rohit in English, as we do not have the total marks T.
Since Statement I alone is sufficient to determine the marks obtained by Rohit in English, while Statement II is not, we conclude that the answer is based solely on Statement I.
Rohit scored 42 marks in English.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
One-third of Ramesh's marks in Arithmetic is equal to half his marks in English. If he gets 150 marks in the two subjects together, how many marks has he got in English?
A60B120C30D50 - Question 2 - Select One
Sunny Gupta scored x marks in Maths, y marks in Hindi and 40 marks in English. What is his total score is these three subjects ?
A100−(x+y)B100−(x+y+40)Cx+y−40Dx+y+40 - Question 3 - Select One
Study the following table carefully to answer these questions
Percentage of marks obtained by six students in six different subjects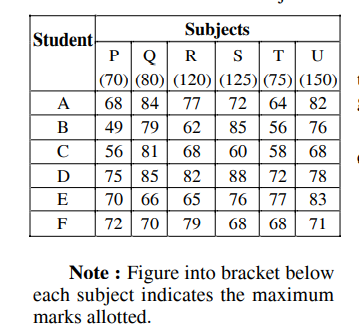
What is the total marks obtained by D in all the subjects together?A449⋅8B499⋅9C480D490
A third of Arun’s marks in Mathematics exceeds a half of his marks in English by 30. If he got 240 marks in the two subjects together, how many marks did he get in English?
View SolutionIn a class test , the sum of Arun's marks in Hindi and English is 30 . Had he got 2 marks more in Hindi and 3 marks less in English , the product of the marks would have been 210 . Find his marks in the two subjects .
View SolutionThe given pie chart shows the marks obtained (in degrees) by a student in different subjects . The total marks obtained by the student in the examination is 432.
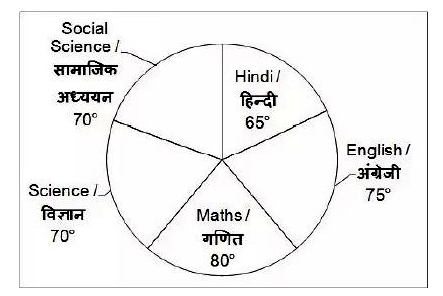
The marks obtained in English is what percentage of the total marks?View SolutionThe total marks obtained by Arun in English and Mathematics are 170. If the difference between his marks in these two subjects Is 10, then the ratio of his marks in these subjects is:
View SolutionA student got 430 marks in five subjects. How many marks did he get in English ?
(I) His average marks in other four subjects is 84.
(II) His marks in English is 8 more than his average marks in five subject.View Solution

