Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
The correct Answer is:A
As shown in figure, each mass experiences three forces namely F, F and F.
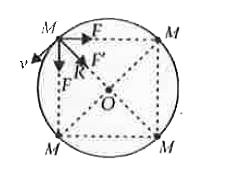
Here, F = force between two masses at separation.
F. = force between two masses at 2R separation.
As all particles move in the circular path of radius R due to their mutual gravitational attraction. Then net force on mass M = mass x centripetal acceleration.
(from figure)
or
or
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)19videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)6videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)9videos
GRAVITATION
- BOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)11videos
BEHAVIOUR OF PERFECT GAS AND KINETIC THEORY
- BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs31videos
KINEMATICS
Similar Questions
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
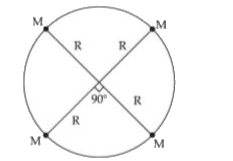 View Solution
View SolutionFor particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles each of mass M and equidistant from each other move along a circle of radius R under the action of their mutual gravitional attraction the speed of each particle is
A√GM2RB12R√1GMC12√GMRD√4GMR - Question 2 - Select One
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2) - Question 3 - Select One
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
AGmRB√2√2GMRC√GMR(2√2+1)D√GMR2√2+14
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.View SolutionTwo particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View Solution

