The acceleration of a particle is given by a (t)=(3.00 m/s2−(2.00ms3))t. (a) Find the initial speed v0 such that the particle will have the same x -coordinate at t =5.00 as it had at t=0. (b)What will be the velocity at t =5.00s?Solution in Telugu
(a)0.833 m/s (b)-9.17 m/s
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Question for descriptiv Answers6videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Short answer type question12videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)22videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER7videos
MOTION IN A PLANE
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III45videos
MOVING CHARGES AND MAGNETISM
Similar Questions
Three tortoises are located at the verties of an equilateral triangle whose side equals a.They all start moving simultaneously with velocity v constant in modulas with first tortise heading continually for the second,the second for the third and third for the first .They will meet after time
04:12View SolutionIf the average velocity of an object is zero some time interval,What can you say about the displacement of the object for that interval?
04:31View SolutionA motor vehicle travelled the first third of a distance s at a speed of v1=10 kmph, the second third at a speed of v2=20 kmph and the last third at a speed of v3=60kmph determine the mean speed of the vehicle over the entire distances.
07:12View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
09:19View SolutionA proton, a deuteron and an a particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field is
05:02View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v= (10+ 5t -t^2) At time t=0, x=0. Find (a) acceleration of particle at t = 2 s and (b) x-coordinate of particle at t=3s
03:49View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
05:06View SolutionThe acceleration of a particle moving along x-direction is given by equation a=(3-2t) m//s^(2) . At the instant t=0 and t=6 s , it occupies the same position. (a) Find the initial velocity v_(o) (b) What will be the velocity at t=2 s ?
03:44View SolutionAn object moves such that is acceleration is given as a=3−2t. Find the initial speed of the object such that the particle will have the same x-coordinate at t=5.0s as it had at t=0. Also find the object's velocity at t=5.0s.
03:52View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
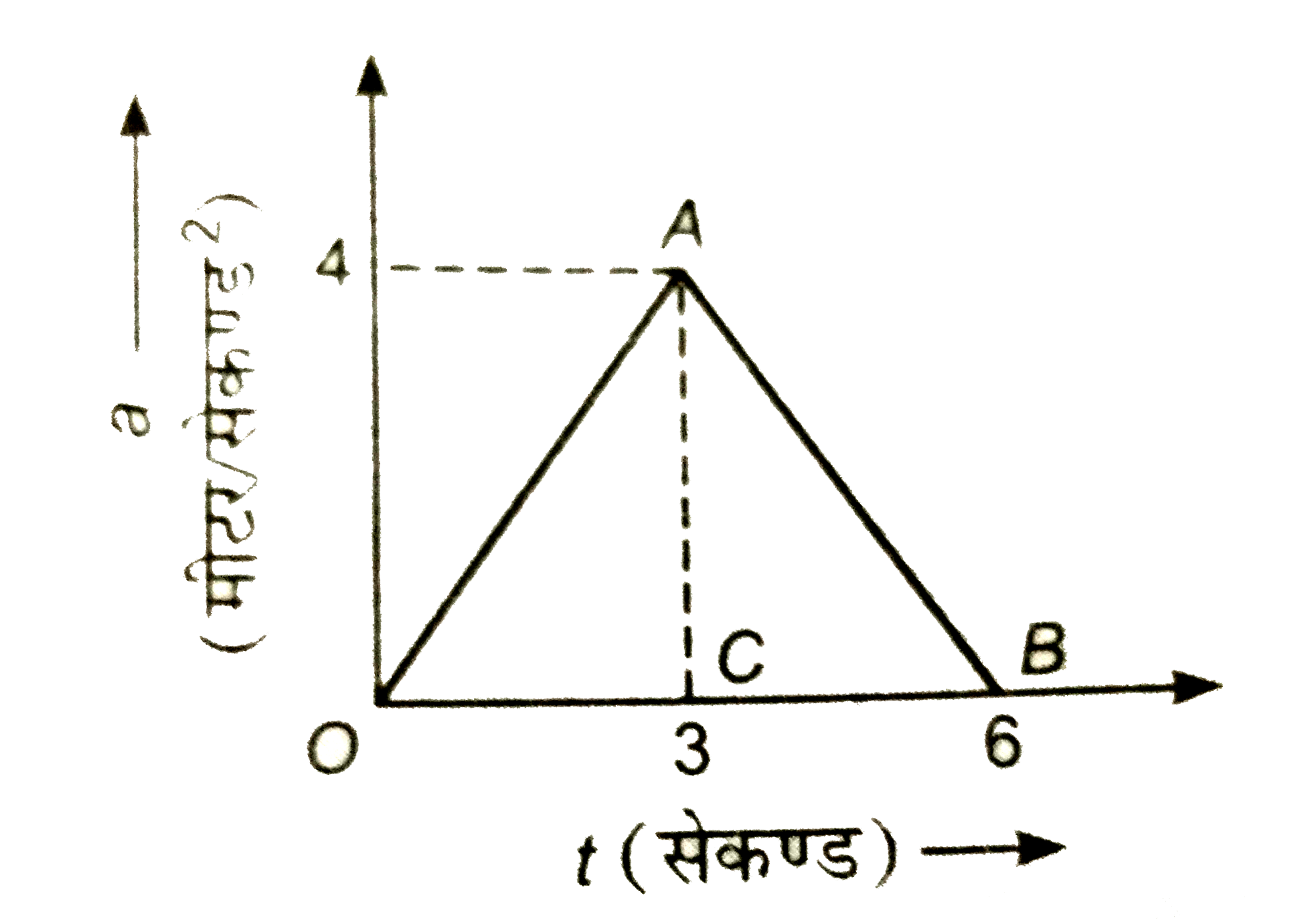 12:57View Solution
12:57View Solutionएक कण t = 0 से चलना प्रारंभ करता है । t समय में कण द्वारा चली हुई दुरी s=(2.5m/s2)t2 से प्राप्त होती है । (a) समय t = 0 से 4 .0 तक में कण की औसत चाल बताएँ। (b) t = 4. 0 s पर कण की चाल बताएँ।
03:56View SolutionA particle moves along x-axis and its acceleration at any time t is a = 2 sin (πt), where t is in seconds and a is in m/s2 . The initial velocity of particle (at time t = 0) is u = 0.
Q. Then the distance travelled (in meters) by the particle from time t = 0 to t = 1 s will be :04:39View SolutionAcceleration of a particle is increasing linearly with time. Its acceleration is 10 m//s^(2) at t =0 and 20 m//s^(2) at t = 5s. "Also" , its speed is 5m/s at t =0 and its positions is x= -100m at t =0 .Find at time t its acceleration ,velocity and positions.
View SolutionThe acceleration of a particle varies with time t as a=t^(2)+t+2 where t is in seconds. The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
03:10View SolutionThe position of a particle moving along the x axis is given in centimeters by x=9.75+1.50t3, where t is in seconds. Calculate (a) the average velocity during the time interval t=2.00s to t=3.00s, (b) the instantaneous velocity at t=2.00s , (c) the instantaneous velocity at t=3.00s, (d) the instantaneous velocity at t=2.50s, and (e) the instantaneous velocity when the particle is midway between its positions at t=2.00s and t=3.00s . (f) Graph x versus t and indicate your answers graphically
03:37View Solution

