A particle moving along straight line has velocity where s is in the displacement . If then which of the following graph best represent s versus t
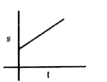
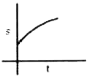
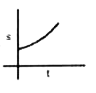
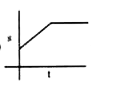
The correct Answer is:C
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
79 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
Knowledge Check
For a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
Ac2s0Bcs0Cc2s−1Dcs−1The velocity-time graph of a body moving along straight line is as follows :
The displacement of the body in 5 s is
 A5 mB2 mC4 mD3 m
A5 mB2 mC4 mD3 mThe equation of a particle moving along a straight line is s=2t3–9t2+12t, where the units of s and t are cm and s. the acceleration of the particle will be zero after
A32 sB23sC12sD1s
A particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionA particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionA particle is moving in a straight line according to the law S=t3+2t2+3t−4, where S is displacement and t is time. Find the velocity and acceleration when t=2.
View SolutionA particle is moving in a straight line such that dv/dt=−λv, where v is the velocity and λ is a constant. At t=0, the particle is at the origin and moves with velocity v0. Sketch the following graphs:
(a)v−t(b)s−t(c)v−s(d)logevv/st
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View Solution
