A particle moving along straight line has velocity v=μs where s is in the displacement . If s=s0 then which of the following graph best represent s versus t
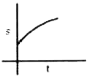
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the velocity v and the displacement s given by the equation v=μs. We will derive the expression for displacement s as a function of time t and then identify the appropriate graph that represents this relationship.
1. Understand the given relationship:
We are given that the velocity v of a particle is proportional to its displacement s such that:
v=μs
where μ is a constant.
2. Relate velocity to displacement:
We know that velocity v can also be expressed as the rate of change of displacement with respect to time:
v=dsdt
Therefore, we can equate the two expressions for velocity:
dsdt=μs
3. Rearrange the equation:
We can rearrange this equation to separate variables:
dss=μdt
4. Integrate both sides:
Now we will integrate both sides. The left side will be integrated with respect to s and the right side with respect to t:
∫dss=∫μdt
This gives us:
ln|s|=μt+C
where C is the constant of integration.
5. Solve for the constant:
To find the constant C, we use the initial condition. At t=0, the displacement s=s0:
ln|s0|=C
6. Substitute back to find s:
Substituting C back into the equation, we have:
ln|s|=μt+ln|s0|
Exponentiating both sides gives:
|s|=eμt⋅|s0|
Thus, we can express s as:
s=s0eμt
7. Identify the graph:
The equation s=s0eμt represents an exponential growth function. At t=0, s equals s0, and as t increases, s increases exponentially. The graph of s versus t will be an upward-curving exponential graph starting from the point (0,s0).
Conclusion:
The graph that best represents s versus t is an exponential curve starting at s0 when t=0 and increasing as t increases.
We are given that the velocity v of a particle is proportional to its displacement s such that:
v=μs
where μ is a constant.
We know that velocity v can also be expressed as the rate of change of displacement with respect to time:
v=dsdt
Therefore, we can equate the two expressions for velocity:
dsdt=μs
We can rearrange this equation to separate variables:
dss=μdt
Now we will integrate both sides. The left side will be integrated with respect to s and the right side with respect to t:
∫dss=∫μdt
This gives us:
ln|s|=μt+C
where C is the constant of integration.
To find the constant C, we use the initial condition. At t=0, the displacement s=s0:
ln|s0|=C
Substituting C back into the equation, we have:
ln|s|=μt+ln|s0|
Exponentiating both sides gives:
|s|=eμt⋅|s0|
Thus, we can express s as:
s=s0eμt
The equation s=s0eμt represents an exponential growth function. At t=0, s equals s0, and as t increases, s increases exponentially. The graph of s versus t will be an upward-curving exponential graph starting from the point (0,s0).
The graph that best represents s versus t is an exponential curve starting at s0 when t=0 and increasing as t increases.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View Solution
An object starts at the origin in a straight line. Its velocity versus time graph is shown in the figure. Which one of the following choices best gives the proper intervals (s) of time for which the object is moving away from the origin?
View SolutionA particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA particle moving in a straight line has velocity-displacement equation as v=5√1+s. Here v is in ms−1 and s in metres. Select the correct alternative.
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
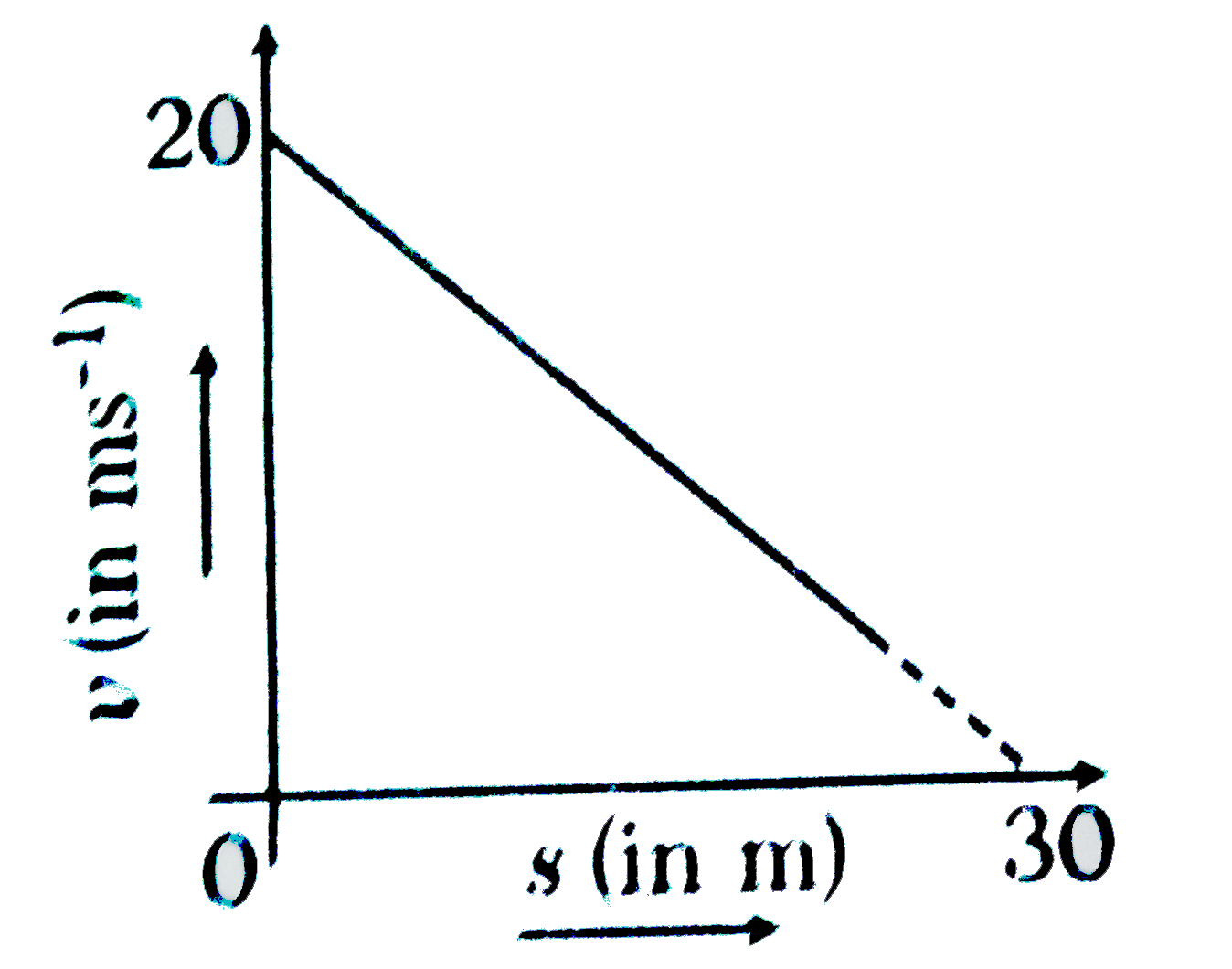
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
View Solution
