A block is placed on a ramp of parabolic shape given by the equation y=x2/20. If μs=0.5, then the maximum height above the ground at which the block can be placed without slipping is
Let the block can be placed on the ramp at a height h above the ground and θ is inclination of the ramp at the position. In the position the component of weight along the slope of ramp is mg sin θ downwards.

The limiting frictional force is =μsN=μsmgcosθ
In equilibrium, mgsinθ=msmgcosθqmgsinθ=tanθ=ms=0.5
but, y=x2/20
Slope tanθ=dydx=2x20=x10
x10=0.5⇒x=5
From the figure maximum height.
h=ymax=x220=2520=1.25m
Similar Questions
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View SolutionA block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
View Solution
Knowledge Check
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
A(a) 16mB(b) 23mC(c) 13mD(d) 12mA block of mass m is placed on a surface with a vertical cross section given by y=x3/6. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is :
A1/2mB16mC2/3D1/3mA disc of radius is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
A2cmB3cmC4 cmD6cm
A block of mass 'm' is placed on a rough surface with a vertical cross section of y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is .
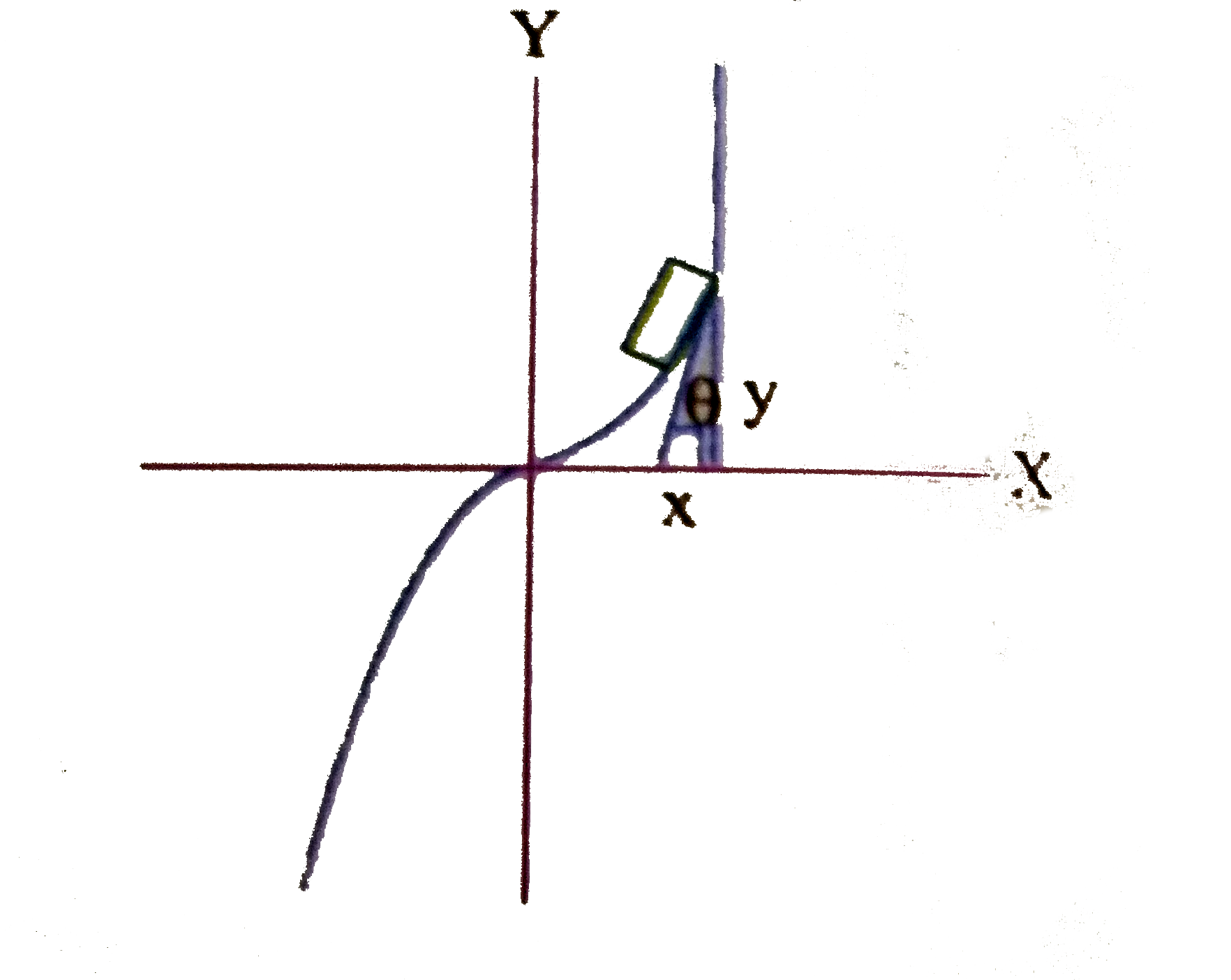
View SolutionA block of mass m is palced on a surface having coefficient of frictionn 0.25, with a vertical cross section given by y=x416. Calculate the maximum height above the ground t which block can be placed without slipping.
View SolutionA disc of radius 5 m is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
View SolutionA parabolic bow1 with its bottom at origin has the shape y=x220 where x and y are in metre The maximum height at which a small mass m can be placed on the bowl without slipping is (coeff of static friction 0.5
 .
.
View SolutionA parabolic bow1 with its bottom at origin has the shape y=x220 where x and y are in metre The maximum height at which a small mass m can be placed on the bowl without slipping is (coeff of static friction 0.5
 .
.
View Solution
