A body is released from rest from the top of an inclined plane of length 'L' and angle of inclination 'θ'. The top of plane of length 1nL(n>1) is smooth and the remaining part is rough. If the body comes to rest on reaching the bottom of the plane then find the value of coefficient of friction of rough plane.
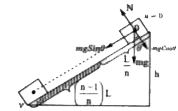
For smooth part :
V2=2a1Ln
For rough part : 0−V2=2a2(n−1n)L
2a1Ln=−2a2(n−1n)L
gsinθ=−g(sinθ−μcosθ)(n−1)
gsinθ[1+n−1]=μgcosθ(n−1)
μ=tanθ[nn−1].
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I
151 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
117 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
6 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
16 Videos
Similar Questions
A body is released from rest from the top of an inclined plane of length L and angle of inclination θ ,.The top of plane of length LN (N>1) is smooth and the remaining part is rough.If the body comes to rest on reaching the bottom of the plane, then the value of coefficient of friction of rough surface is ?
View SolutionIf the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View Solution
Knowledge Check
A block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
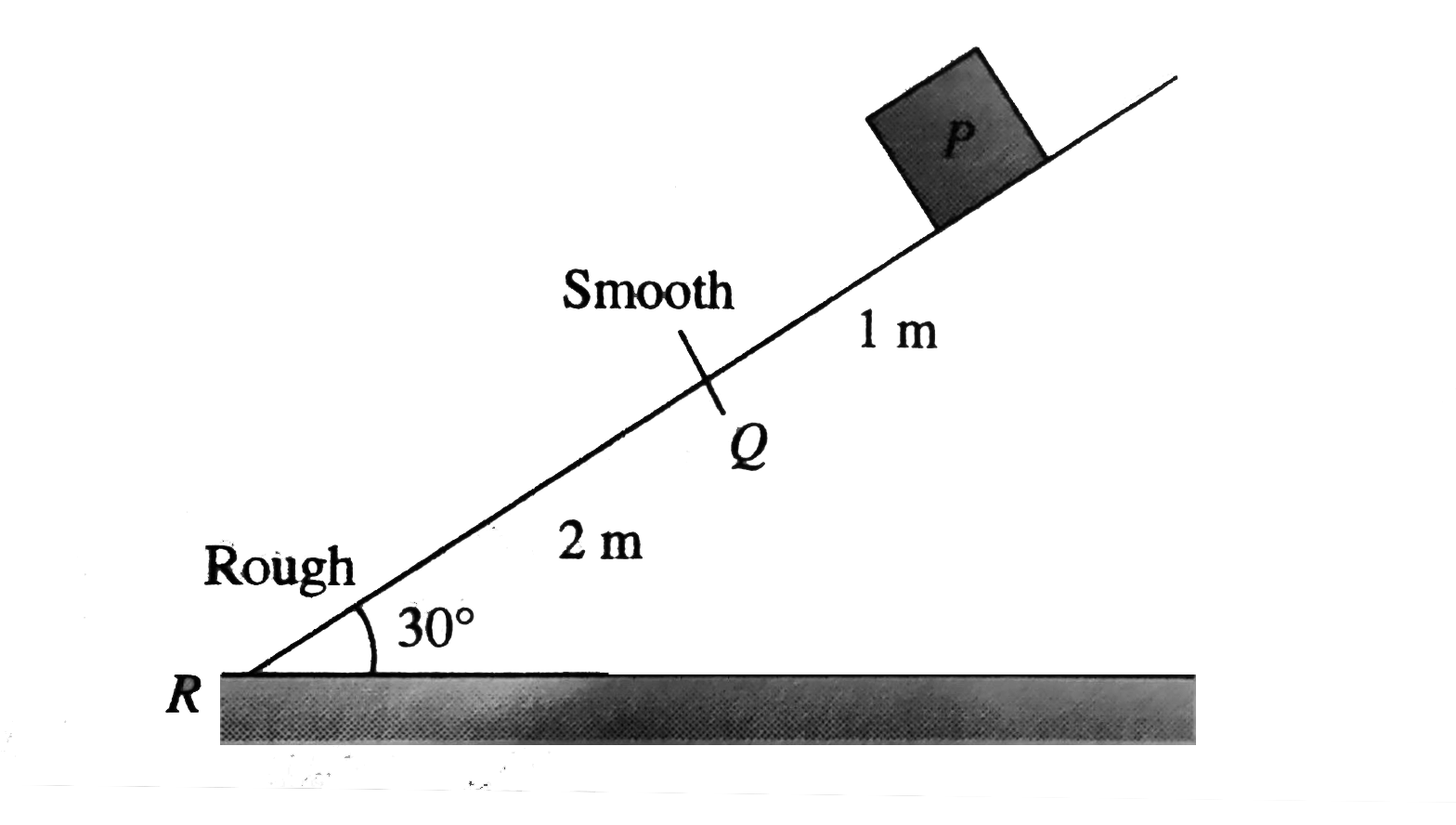 A(a) 2√3B(b) √32C(c) √34D(d) √35
A(a) 2√3B(b) √32C(c) √34D(d) √35A body is allowed to slide from the top along a smooth inclined plane of length 5m at an angle of inclination 30∘.If g=10ms−2, time taken by the body to reach the bottom of the plane is
A√32sB1.414sC1√2sD2sA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclination is doubled for the same length of the plane, what will be the velocity of the body on reaching the ground
AvB2vC(2cosθ)12vD(2sinθ)12v
The upper half of an inclined plane with an angle of inclination theta, is smooth while the lower half is rough. A body starting from rest at the top of the inclined plane comes to rest at the bottom of the inclined plane. Then the coefficient of friction for the lower half is
View SolutionA block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.

View Solution
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View SolutionA uniform disc is released from the top of a rough inclined plane of angle θ and height h. The coefficient of friction between the disc and the plane is μ=tanθ4. The speed of centre of mass of disc on reaching the bottom of the plane is
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View Solution
