The upper half of an inclined plane with an angle of inclination theta, is smooth while the lower half is rough. A body starting from rest at the top of the inclined plane comes to rest at the bottom of the inclined plane. Then the coefficient of friction for the lower half is
μ=2tanθ
μ=tanθ
μ=2tanθ
μ=1tanθ
The correct Answer is:A
To solve the problem, we need to analyze the motion of a body on an inclined plane that has both smooth and rough sections. Here’s a step-by-step solution:
Step 1: Understand the Problem
The inclined plane has two sections: the upper half is smooth, and the lower half is rough. A body starts from rest at the top and comes to rest at the bottom. We need to find the coefficient of friction (μ) for the lower half.
Step 2: Define the Variables
- Let the angle of inclination be θ.
- Let the total distance of the inclined plane be d. Therefore, each half of the inclined plane is d/2.
- The initial velocity (u) at the top is 0, and the final velocity (v) at the bottom is also 0.
Step 3: Calculate Velocity at the Middle Point
Using the kinematic equation:
v2=u2+2as
where:
- u=0
- a=gsinθ (acceleration down the smooth incline)
- s=d2
Substituting the values:
v2=0+2(gsinθ)(d2)
v2=gdsinθ
Step 4: Analyze the Lower Half of the Incline
In the lower half, the forces acting on the body are:
- Gravitational force component down the incline: mgsinθ
- Frictional force acting up the incline: f=μmgcosθ
Using Newton's second law:
ma′=mgsinθ−μmgcosθ
Dividing by m:
a′=gsinθ−μgcosθ
Step 5: Apply Kinematic Equation for the Lower Half
Using the kinematic equation again for the lower half:
v′2=u′2+2a′s
where:
- v′=0 (final velocity at the bottom)
- u′=v (initial velocity at the middle point)
- s=d2
Substituting the values:
0=v2+2(gsinθ−μgcosθ)(d2)
Substituting v2=gdsinθ:
0=gdsinθ+2(gsinθ−μgcosθ)(d2)
Step 6: Simplify the Equation
Rearranging gives:
0=gdsinθ+gdsinθ−μgdcosθ
0=2gdsinθ−μgdcosθ
Step 7: Solve for μ
Dividing through by gd (assuming g and d are not zero):
0=2sinθ−μcosθ
Rearranging gives:
μcosθ=2sinθ
Thus:
μ=2sinθcosθ
μ=2tanθ
Final Answer
The coefficient of friction for the lower half of the inclined plane is:
μ=2tanθ
---
The inclined plane has two sections: the upper half is smooth, and the lower half is rough. A body starts from rest at the top and comes to rest at the bottom. We need to find the coefficient of friction (μ) for the lower half.
- Let the angle of inclination be θ.
- Let the total distance of the inclined plane be d. Therefore, each half of the inclined plane is d/2.
- The initial velocity (u) at the top is 0, and the final velocity (v) at the bottom is also 0.
Using the kinematic equation:
v2=u2+2as
where:
- u=0
- a=gsinθ (acceleration down the smooth incline)
- s=d2
v2=0+2(gsinθ)(d2)
v2=gdsinθ
In the lower half, the forces acting on the body are:
- Gravitational force component down the incline: mgsinθ
- Frictional force acting up the incline: f=μmgcosθ
ma′=mgsinθ−μmgcosθ
Dividing by m:
a′=gsinθ−μgcosθ
Using the kinematic equation again for the lower half:
v′2=u′2+2a′s
where:
- v′=0 (final velocity at the bottom)
- u′=v (initial velocity at the middle point)
- s=d2
0=v2+2(gsinθ−μgcosθ)(d2)
Substituting v2=gdsinθ:
0=gdsinθ+2(gsinθ−μgcosθ)(d2)
Rearranging gives:
0=gdsinθ+gdsinθ−μgdcosθ
0=2gdsinθ−μgdcosθ
Dividing through by gd (assuming g and d are not zero):
0=2sinθ−μcosθ
Rearranging gives:
μcosθ=2sinθ
Thus:
μ=2sinθcosθ
μ=2tanθ
The coefficient of friction for the lower half of the inclined plane is:
μ=2tanθ
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionThe upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View Solution
Knowledge Check
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1
The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionThe upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionThe upper half of an inclined plane of inclination θ is perfectly smooth while lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom, if the coefficient of friction between the block and lower half of the plane is given by
View SolutionThe upper portion of an inclined plane of inclination a is smooth and the lower portion is rough. A partical slide down from rest the top and just comes to rest at the foot . If the ratio of smooth length to rough length is m:n, find the coefficient of friction .
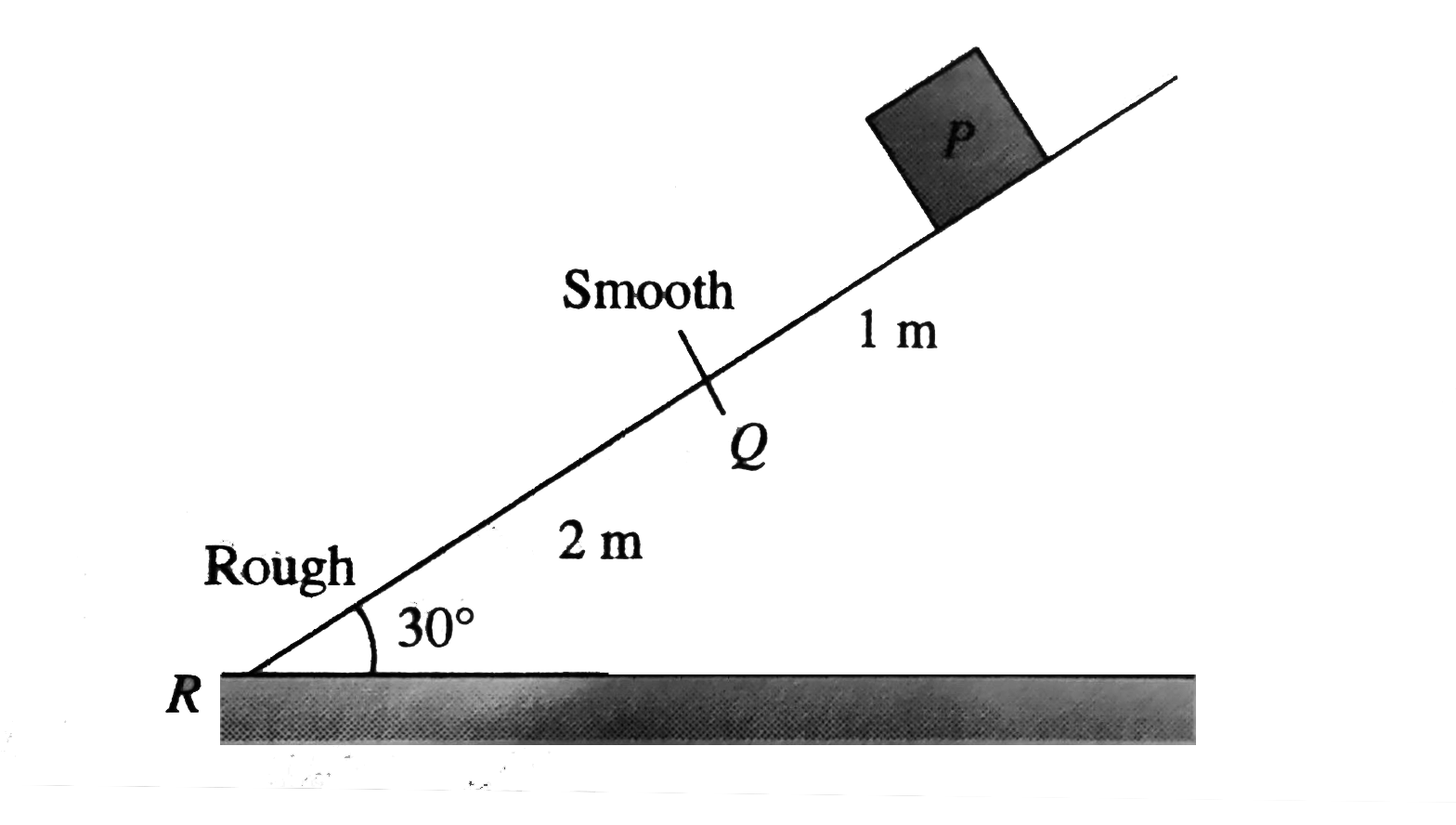
View SolutionA block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
View SolutionA body is slipping from an inclined plane of height h and length l . If the angle of inclination is θ , the time taken by the body to come from the top to the bottom of this inclined plane is
View SolutionA block is kept on a inclined plane of inclination θ of length l. The velocity of particle at the bottom of inclined is (the coefficient of friction is μ
View Solution
