Obtain Gauss's law from the flux associated with a sphere of radius r and charge 'q' at centre.Solution in Gujrati
Let us consider the total fiux through a sphere of radius r, which encloses a point charge q at its centre.
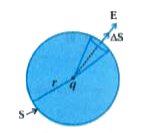
Divide the sphere into small area elements, as shown in figure.
The flux through an area element is,
where we have used Coulomb.s law for the electric field due to a single charge q.
The unit vector is along the radius vector from the centre to the area element.
The area element and have the same direction,
The total flux through the sphere is obtained by adding up flux through all the different area elements.
( for sphere)
Gauss.s law: Electric flux through a close surface S.
= total charge enclosed by S.
The electric flux associated with any close surface is equal to the ratio of net charg, enclosed by surface to
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (APPLICATION OF GAUSS.S LAW)
1 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (FIELD DUE TO AN INFINITELY LONG STRAIGHT UNIFORMLY CHARGED WIRE)
1 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (CONTINOUS CHARGE DISTRIBUTION)
4 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)
1 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )
38 Videos
Similar Questions
Mention applications of Gauss's law.
View SolutionObtain the expression of electric field by a straight wire of infinite length and with linear charge density λ.
View SolutionExplain linear charge density, surface charg density and volume charge density for uniformly charge distribution.
View SolutionMass of photon in motion is ………
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......

View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View SolutionAssertion. A charge q is placed on a hieght h//4 above the centre of a square of side b . The flux associated with the square is independent of side length. Reason. Gauss's law is independent fo size of the Gaussian surface.
View SolutionAn unchanged conducting sphere of radius R is placed near a uniformly charge ring of radius R. Total charge on ring is Q. The centre of sphere lies on axis of ring and distance of centre of sphere from centre of ring is R
View SolutionA sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
View SolutionFlux (ph) as a function of distance (r) from centre of uniformly charged solid sphere of charge Q and radius R , is best represented by
View SolutionFlux associated with the cap of a sphere having semi-vertical (semi- vertex) angle alpha and let charge Q is placed at centre is
View SolutionThe centre of neutral conducting sphere of radius "R" is at distance 'd' from a point charge "Q" .The potential of the sphere is
View SolutionA sphere of radius R, is charged uniformly with total charge Q. Then correct statement for electric field is (r = distance from centre): -
View SolutionA Gausian sphere of radius r intercepts a line with a uniform charge density +1 as shown. The line is at a distance root 3'r/2 from the centre of the sphere. What is the electric flux associated with the Gaussian sphere?
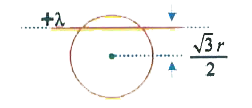
View SolutionA point charge +Q is placed at a point. Calculate the electric flux associated with one sphere of radius r , which the given point charge at its centre.
View Solution
