Obtain the expression of electric field by a straight wire of infinite length and with linear charge density λ.Solution in Gujrati
Consider an infinitely long thin straight wire with uniform linear charge density λ
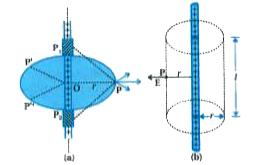
Suppose we take the radial vector from O to P and rotate it around the wire. The points P P., P" so obtained are completely equivalent with respect to the charged wire.
This implies that the electric field must have the same magnitude at these points.
The direction of electric field at every point must be radial (outward if λ>0, inward λ<0 ).
Since the wire is infinite, electric field does not depend on the position of P along the length of the wire.
The electric field is everywhere radial in the plane cutting the wire normally and its magnitude depends only on the radial distance r.
Imagine a cylindrical Gaussian surface as shown in figure.
Since the field is everywhere radial, flux through the two ends of the cylindrical Gaussian surface is zero.
At the cylindrical part of the surface E is normal to the surface at every point and its magnitude is constant since it depends only on r.
The surface area of the curved part is 2nd, where I is the length of the cylinder.
Flux through the Gaussian surface, = flux through the curved cylindrical part of the surface
=E×2πrl
The surface includes charge equal to λl. Gauss.s law then gives,
E×2πrl=λlε0
∴E=λ2πε0r
∴→E=λ2πε0rˆn
where ˆn is the radial unit vector in the plane normal to the wire passing through the point.
→E is directed outward if λ is positive and inward if λ is negative.
Note that it is impossible to find electric field at any point due to wire of infinite length, but here electric field is expressed at a point with effect of central part of wire and effect of ends is ignored.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (FIELD DUE TO AN UNIFORMLY CHARGED INFINITE PLANE SHEET)1videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (FIELD DUE TO A UNIFORMLY CHARGED THIN SPHERICAL SHELL)6videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (APPLICATION OF GAUSS.S LAW)1videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )38videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Obtain the expression of electric field by a plane of infinite size and with uniform charge distribution.
06:46View SolutionObtain the expression of electric field by thir spherical shell with uniform charge distribution at a point outside it.
02:45View SolutionMention applications of Gauss's law.
03:14View SolutionMass of photon in motion is ………
11:26View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......
 View Solution
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density lambda is directly proportional to
05:11View SolutionThe electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
 07:18View Solution
07:18View Solutionएक अनन्त लम्बाई के एकसमान आवेशित सीधे तार का रेखिक आवेश धनत्व 10.0×10−8 कूलाम/ मीटर है तार से 2 सेमी दुरी पर उत्पन्न विधुत क्षेत्र की तीव्रता गीत कीजिए ।
00:46View Solutionअनंत लम्बाई के किसी सीधे कुचालक तार पर एकसमान रूप से आवेश वितरण के कारण इसका रैखिक घनत्व λ है | एक सिरे से लाम्बिक दुरी R पर परिणामी विद्युत - क्षेत्र के लिए व्यंजक प्राप्त करे |
View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View SolutionObtain the expression for electric field due to an infinitely long charged wire .
03:37View Solutionगॉस प्रमेय की सहायता से एकसमान रूप से आवेशित अनन् लम्बाई के सीधे तार के निकट वैद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए।
अथवा गॉस के नियम से एक अनन्त लम्बाई के आवेशित तार के कारण किसी बिंदु पर वैद्युत क्षेत्र की तीव्रता के लिए व्यंजक प्राप्त कीजिए।
अथवा गॉस नियम की सहायता से एक आवेशित लंबे तार के निकट वेद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त कीजिए । तार का रेखीय आवेश घनत्व λ कूलॉम/मीटर है।03:26View SolutionElectric field at a point of distance from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
05:26View SolutionState Gauss' law in electrostatic. Using it derive an expression for the electric field due to an infinitely long straight wire of linear charge density lambda C/m.
03:22View SolutionState Gauss' law.Using this law obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density lambda (ii) A wire AB of length L has linear charge lambda =kx, where x is measured from the end A of the wire. The wire is enclosed by a Gaussian hollow surface.Find the expression for the electric flux through the surface.
09:07View Solution

