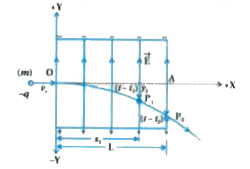
A particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in figure. The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/(2mv2x).
Compare this motion with motion of a projectile in gravitational field discussed in Section 4.10 of Class XI Textbook of Physics.
 Solution in Gujrati
Solution in Gujrati
Consider vertically upward electric field →E between two horizontal plates as shown in the figure.
A particle of mass m and charge - q, enters this electric field along X-axis with constant horizontal velocity vx at time t = 0. Because of negative charge, it gets deflected towards positive plate. Suppose it passes through points P1 and P2 at time t1 and t2 respectively. At time t2, horizontal displacement of given charge is equal to L. Here, no force is exerted on this charge along horizontal direction and so its horizontal velocity vx reminas constant.
∴vx=Lt2⇒t2=Lvx..........(1)
Here electric force exerted on given charge is,
Fe=(−q)E=may⇒ay=−qEm.......(2)
At time t2 if vertical displacement of given charge is,
y=v0yt2+12ayt22
∴y=−12(qEm)L2v2x⇒|y|=12(qEm)L2v2x......(3)
Above equation gives required result. Here, displacement of given charge is towads - Y-axis and so y is negative. Comparison with projectile motion : Here, at the end of time t1 horizontal displacement of given charge is x1 and so,
vx=x1t1⇒t1=x1v1...........(4)
At the end of time t1 vertical displacement of given charge is,
y1=(v0)t1+12ayt21
∴y1=−qE2mv2xx21y1=x21 ...............(5)
Above equation is similar to equation of projectile motion.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION B NUMERICALS (NUMERICAL FOR .DARPAN. BASED ON TEXTBOOK)8videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION C NCERT EXEMPLAR SOLUTION (MULTIPLE CHOICE QUESTIONS (MCQs))7videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION B NUMERICALS (NUMERICAL FROM TEXTUAL EXERCISES)24videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )38videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two spheres of copper, having mass 1 g each, are kept 1 m apart. The number of electrons in them are 1 % less than the number of protons. The electrical force between them is Atomic wt. of copper is 63.54 g/mol, atomic number is 29, Avogadro's number NA=6.023×1023mol−1 and k=9×109 SI
View SolutionIn figure, two positive charges q2 and q3 fixed along the y-axis, exert a net electric force in the + x direction on a charge q1 fixed along the x-axis. If a positive charge Q is added at (x, 0), the force on q1
 02:31View Solution
02:31View SolutionWhat is the force between two small charged spheres having charges of 2×10−7C and 3×10−7 C placed 30 cm apart in air ?
10:07View SolutionMass of photon in motion is ………
06:20View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......
 06:26View Solution
06:26View SolutionA paraticale of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx. The length of plate is L and a uniform electric field E is maintained between the plates. Show that the verticale deflection of the particle at the far edge of the plate is qEL2/(2mv2x). Compare this motion with motion of a projectille in gravitional field.
05:02View SolutionBetween two horizontal parallel plates, uniform electric field E directed vertically downward. A charged particle (q,m) remains in equilibrium in vaccum between the plates. Find shortage/excess of electrons in the charged particle .
07:43View Solutionप्रारम्भ में, x-अक्ष के अनुदिश vx चाल से गति करती हुए दो आवेशित प्लेटो के मध्य क्षेत्र में m द्रव्यमान तथा -q आवेश का कण प्रवेश करता है। प्लेटो की लम्बाई L है। इन दोनों प्लेटो के बीच एकसमान विधुत क्षेत्र E बनाए रखा जाता है। दर्शाइए की पटेल के अंतिम किनारे पर कण का उध्र्वाधर विक्षेप qEL2/(2mv2x) है।
03:28View SolutionA particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed V_(x) (as in the fig.). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL^(2)//(2mV_(x)^(2)) . Compare this motion with motion of a projectille in gravitational field discussed in section 4.10 of 1^(st) Year Textbook of Physics.
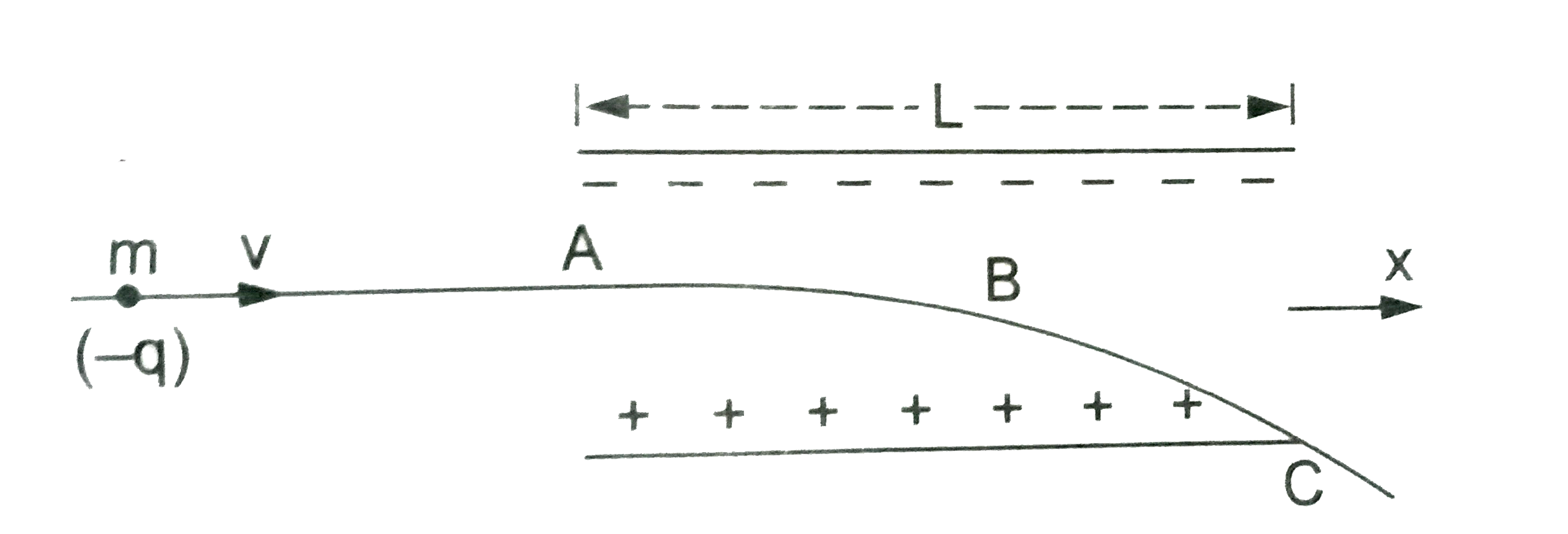
View Solutionद्रव्यमान m तथा आवेश (-q) का एक कण x-अक्ष के अनुदिश v चाल से गतिशील है। दो आवेशित प्लेटों के बीच से गुजरने के क्रम में इसका परवलीय पथ (parabolic path) चित्र में ABC द्वारा दिखाया गया है। यदि प्लेटो की लेबाई L तथा उनके बाच एकसमान विद्युत-क्षेत्र E हो, तो प्लेट के किनारे से निकलते समय तक कण का ऊर्ध्वाधर विक्षेप (vertical deflection) ज्ञात करें।
 07:59View Solution
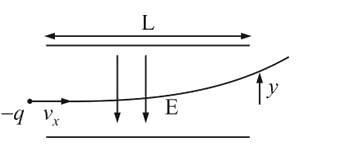
07:59View SolutionA particle of mass m and charge(-q) enters the region between the two charged plates intially moving along x - axis with speed Vx . The length of plate is L and a uniform electric field E is maintained between the plates . Show that the verticles deflection of the particle at the far edge of the palte is qEL2/(2mv2x).
 03:05View Solution
03:05View SolutionA uniform electric field of magnitude E exists in between two parallel metal plates , as shown in the figure given below. One particle of mass m and charge q is projected along the central line between the plates. Particle just missed to strike upper plate , while coming out of plates. Find : (a)Time taken by the particle to come out of plates. (b)Speed of the particle as it comes out of plates. (c) Angle of deviation suffered by particle. The length of the plates is L and the distance between the plates is d. Ignore gravity .
View SolutionA particle of mass m and charge enters the region between the two charged plates initally moving along x axis with speed vx the length of plate is l and an uniform vertical deflectio of the particle at the far edge of the plate is qEL2/2mv2x
compare this motion with motion of a projectile in gravitational field07:16View SolutionA particle of mass m and charge (-q) enters the regions between the two charged plates initially moving along x-axis with speed vx (like particle 1 in.) The length of plate is L and an the particle at the far edge of the plate is qEL2/(2mv2x).
03:06View SolutionA particle of mass m and charge enters the region between the two charged plates initally moving along x axis with speed v_(x) the length of plate is l and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL^(2)//2mv_(x)^(2) compare this motion with motion of a projectile in gravitational field
04:58View Solution

