Two fixed, identical conducting plates (a and (3), each of surface area S are charged to - Q and q, respectively, where Q > q > 0. A third identical plate (λ ), free to move Is located on the other side of the plate with charge q at a distance d as per figure. The third plate is released and collides with the plate f3 . Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst β and γ.

(a) Find the electric field acting on the plate γ before collision.
(b) Find the charges on β and γ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate βSolution in Gujrati
(a) Net electric field at plate γ before collision is vector sum of electric field at plate γ due to plate a and p.
The electric field at plate γ due to plate α is,
→E1=−Q(S(2ε0)(−ˆi))
The electric field at plate γ due to plane β is,
→E2=qS(2ε0)(−ˆi)
∴ Hence, the net electric field at plate γ before collision is,
→E=→E1+→E2=q−QS(2ε0)(ˆi)
∴Q−qS(2ε0) to the field, If Q>q
(b) During collision plates β and γ are in contact with each other, hence their potentials become same.
Suppose charge on plate β is q1 and charge on plate γ is q2. At any point O in between the two plates, the electric field must be zero.
Electric field at O due to plate α,
→Ea=QS(2ε0)(−ˆi)
Electric field at O due to plate β
→E2=q1S(2ε0)(ˆi)
Electric field at O due to plate γ
→Ey=q2S(2ε0)(−ˆi)
As the electric field at O is zero, therefore,
Q+q2S(2ε0)=q1S(2ε0)
∴Q+q2=q1

On solving eq. (1) and (2) we get,
q1=(Q+q2) = Change on plate β
q1=(q2) = charge on plate γ
(c) Let the velocity be v at the distance d from plate β after the collision. If m is the mass of the plate γ, then the gain in K.E. over the round trip must be equal to the work done by the electric field.
→E2=Q2ε0S(−ˆi)+Q+q22ε0Sˆi=q22ε0Sˆi
Just before collision, electric field at plate:
γ is →E1=Q−q2ε0Sˆi
and →F2=→E2.q2=(q2)22ε0Sˆi
Total work done by the electric field is round trip movement of plate γ
W=(F1+F2)d
=(Q−q2)2d2ε0S
If m is the mass of plate γ , the K.E. gained by the plate = 12mv2
According to work energy principle,
12mv2=W⇒12mv2=(Q−q2)2d2ε0S
∴v=(Q−q2)(dmε0S)1/2
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D (MULTIPLE CHOICE QUESTIONS (MCQS)) (MCQS FROM .DARPAN. BASED ON TEXTBOOK) (ELECTROSTATIC ELECTRIC CHARGE AND FRICTIONAL ELECTRICAL CHARGE)55videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION D (MULTIPLE CHOICE QUESTIONS (MCQS)) (MCQS FROM .DARPAN. BASED ON TEXTBOOK) (LECTRIC FIELD AND ELECTRIC DIPOLE)26videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION C NCERT EXEMPLAR SOLUTION (SHORT ANSWER TYPE QUESTIONS)6videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )38videos
ELECTROMAGNETIC INDUCTION
Similar Questions
When any neutral conductor is made charged, its mass ……………………..
View SolutionElectric dipole moment is......quantity.
03:37View SolutionA paisa coin is made up of Al-Mg alloy and weighs 0.75 g. It has a square shape and its diagonal measures 17 mm. It is electrically neutral and contains equal amounts of positive and negative charges.
Treating the paisa coins made up of only Al, find the magnitude of equal number of positive and negative charges. What conclusion do you draw from this magnitude ?08:40View SolutionMass of photon in motion is ………
View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......
 06:00View Solution
06:00View SolutionTwo fixed, identical conducting plates (alpha and beta) , each of surface area S are charged to -Q and q , respectively, where Q gt q gt 0 . A third indentical plate (gamma) , free to move is located on the other side of the plate with charge q at a distance d, fig. The third plate is released and collidies with the plate beta . Assume the collsion is electric and the time of collision is sufficient to redistribute charge amongst beta and gamma . (a) Find the electric field acting on the plate gamma before collision. (b) Find the charge on beta and gamma after the collision. (c) Find the velocity of the plate gamma after the collision and at a distance d from the plate beta .
View Solution
Two large parallel conducting plates of net charge 2Q and −Q are placed in a uniform external electric field Q2Aε0 prependicular to plates as shown. The surface area of each plates is A. The charge on the left surface of the left plate and right surface of the right plate are respectively.09:51View SolutionFour large identical metallic plates are placed as shown in the Figure. Plate 2 is given a charge Q. All other plates are neutral. Now plates 1 and 4 are earthed. Area of each plate is A.
(a) Find charge appearing on right side of plate 3.
(b) Find potential difference between plates 1 and 2.
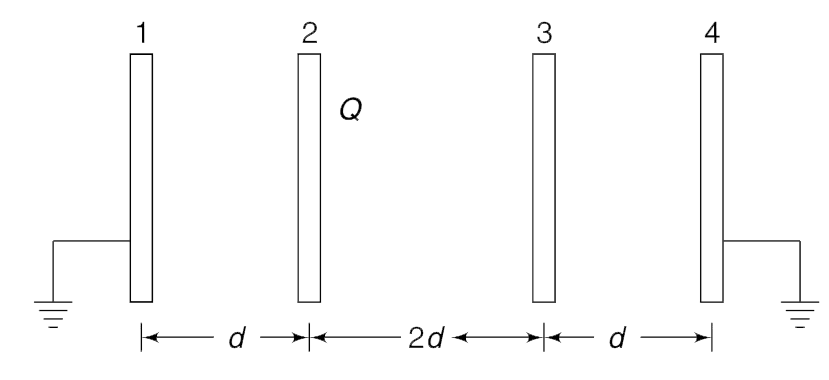 03:29View Solution
03:29View SolutionTwo fixed, identical conducting plates (αandβ), each of surface area S are charged to -Q and q, respectively, where Q > q > 0. A third identical plate (γ), free to move is located on the other side of the plate with charge Q at a distance d (figure). The third plate is released and collides with the plate β. Assume the collision is elastic and the time of collision is sufficient to redistribute charge amongst βandγ.
(a) Find the electric field acting on the plate γ before collision.
(b) Find the charges on βandγ after the collision.
(c) Find the velocity of the plate γ after the collision and at a distance d from the plate β.
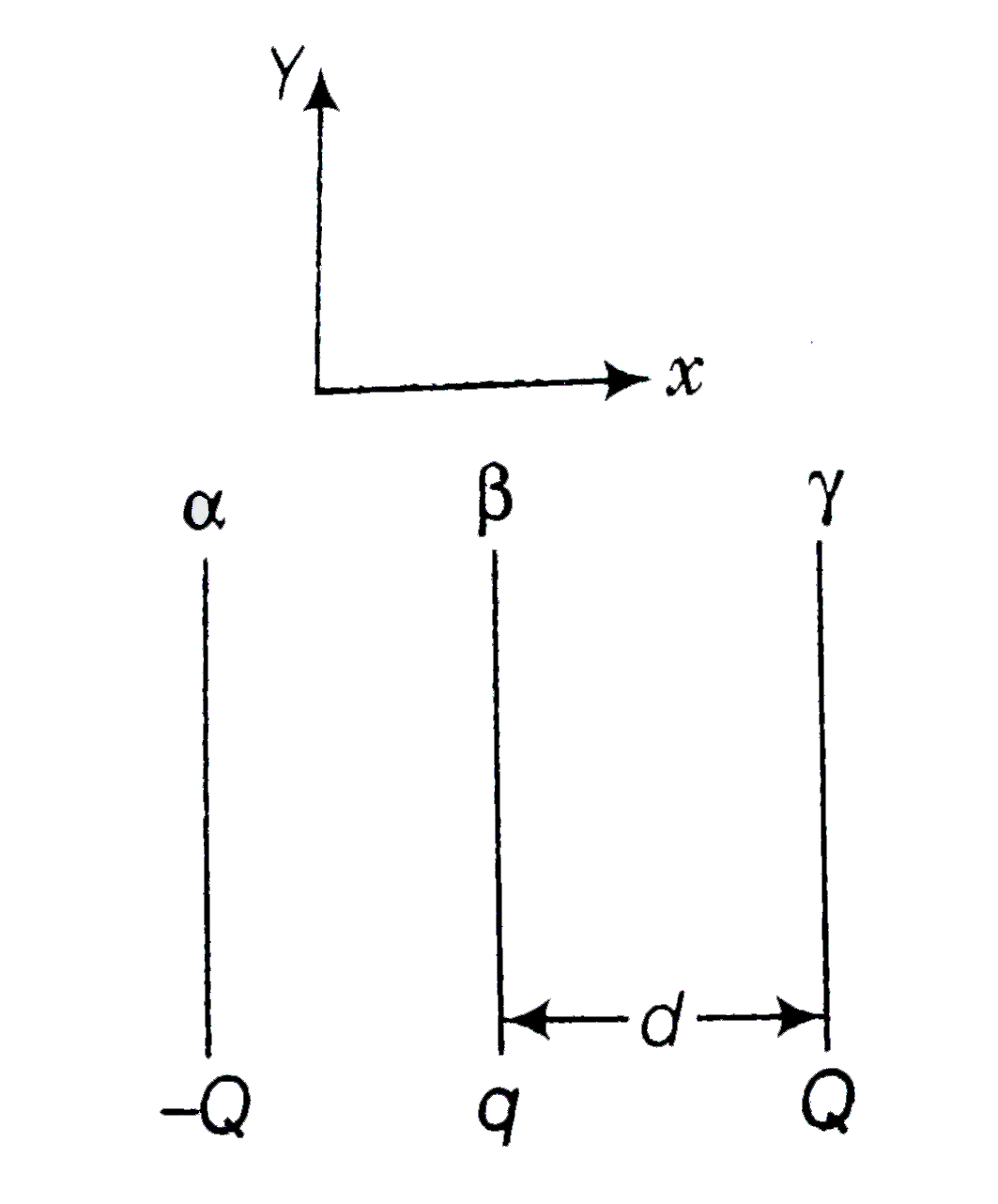 View Solution
View Solutionकिसी समांतर पट्टिका सधारित्र के लिए, प्लेटो का क्षेत्रफल =A प्लेटो के बीच दुरी =d प्लेटो पर आवेश +Q तथा -Q है। यदि प्लेटो के बीच आकर्षण-बल F हो, तब
01:35View SolutionWhat is the force of attraction between the two plates of a parallel plate capacitor? Assume that, area of each plate of the capacitor is A and one plate is charged with +Q and the other with -Q.
07:40View SolutionThree identical metal square plates of surface area A of each side is arranged as shown in the figure.Plates 1 2 and 3 are given charges +20, -Q and -Q respectively. Find out the correct options A) Charge on the two faces of the middle plate are -2Q and Q B) Charge on the two faces of the middle plate are -Q and 0 C) Charge on the two faces of the left most plate are zero and 2Q D) Charge on the two faces of the right most plate are -Q and zero
03:56View Solutionएक समांतर प्लेट संधारित्र में, प्लेट का क्षेत्रफल A तथा आवेश Q है। अन्य प्लेट पर आवेश के कारण एक प्लेट पर लगने वाला बल बराबर होगा :
04:08View SolutionThe plates of a charged parallel plate capacitor attract each other by a force F= ____________, where q = charge on each plate and A = area of each plates.
02:58View SolutionForce between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png) 01:28View Solution
01:28View Solution

