Figure shows a small magnetised needle P placed at a point 0. The arrow shows the direction of its magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.
(a) In which configuration the system is not in equilibrium ?
(b) In which configuration is the system in (i) stable, and (ii) unstable equilibrium ?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown ?

(a) For non-equilibrium state of magnetic needle Q in the magnetic field of P, we should have,
−−→mQ⊥−→BP
For a pair of P and Q1 and for a pair of P and Q2 we have −−→mQ⊥−→BP because
−−→mQ=mQˆi
−→BP=Be(−ˆj)

(Where Be= magnetic field of P on its equator).
(b) (i) For stable equilibrium state of magnetic needle Q in the magnetic field of P, we should have −−→mQ∣∣−→BP
(means →Qand−→BP must be in the same directions)
Here for a pair of P and Q3, we have −−→mQ=mQ(−ˆj)and−→BP=Be(−ˆj)⇒−−→mQ∣∣−→BP
Also for a pair of P and Q6. we have
−−→mQ=mQ(ˆj)and−→BP=Ba(ˆj)⇒−−→mQ∣∣−→BP
(Where Ba= magnetic field of P on its axis)
(ii) For unstable equilibrium state of magnetic needle Q in the magnetic field of P, we should have −−→mQ∣∣(−−→BP) means −−→mQand−→BP must be in opposite directions)
+Here for a pair of P and Q4, we have −−→mQ=mQ(−ˆj)and−→BP=Ba(ˆj)⇒−−→mQ∣∣(−−→BP)
Also for a pair of P and Q5, we have
−−→mQ=mQ(ˆj)and−→BP=Be(−ˆj)⇒−−→mQ∣∣(−−→BP)
(c) For lowest potential energy, system must have stable equilibrium for which we should have −−→mQ∣∣−→BP which is true for a pair of P and Q6.
(Note : Magnetostatic potential energy of P and Q6 is
UPQ6=−mQBacos0∘=−mQ(μ04π2mpr3)
Magnetostatic potential energy of P and Q3 is UPQ3=−mQBecos0∘=−mQ(μ04πmpr3)
Comparing above two values we get, UPQ6<UPQ3
Answer for section (c) would be a pair of P and Q6
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION B Numericals (Numerical From Textual Exercise)
25 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - SECTION B Numericals (Numerical From Textual Exercise) Additional Exercises
19 Videos
- MAGNETISM AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - MAGNETISM AND MATTEREXERCISE - Try Yourself
77 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - KUMAR PRAKASHANCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Section D ( MCQs asked in Cometitive Exams )
39 Videos
- MOVING CHARGES AND MAGNETISMBOOK - KUMAR PRAKASHANCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - SECTION D (MCQs ASKED IN COMPETITIVE EXAMS)
34 Videos
Similar Questions
Figure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionFigure shows a small magnetized needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetized needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionFigure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionConsider the situation shown in the diagram, where A small magnetised needle A is placed at a centre marked, as O. The direction of its mangetic moment I s indicated by arrow. The other arrow show different position (and orientations of the magnetic moment) of antoher identical magnetised eedle X.
In which configuration the system is not in equlibrium?
(ii) In which configuration is the system in (a) stable and (b) unsable equilibrium
(iii) Which configuration corresponds to the lowest potentials energy among all the configuration shown

View SolutionConsider the situation shown in the diagram, where A small magnetised needle A is placed at a centre marked, as O. The direction of its mangetic moment I s indicated by arrow. The other arrow show different position (and orientations of the magnetic moment) of antoher identical magnetised eedle X.
In which configuration the system is not in equlibrium?
(ii) In which configuration is the system in (a) stable and (b) unsable equilibrium
(iii) Which configuration corresponds to the lowest potentials energy among all the configuration shown

View SolutionFigure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionFigure shows a small magnetised needle P placed at a point O. The arrow shows the direction of magnetic moment. The other arrows show different positions (and orientations of the magnetic moment) of another identical magnetised needle Q.

(a) In which configuration is the system not in equilibrium?
(b) In which configuration is the system in (i) stable and (ii) unstable equilibrium?
(c) Which configuration corresponds to the lowest potential energy among all the configurations shown?
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?

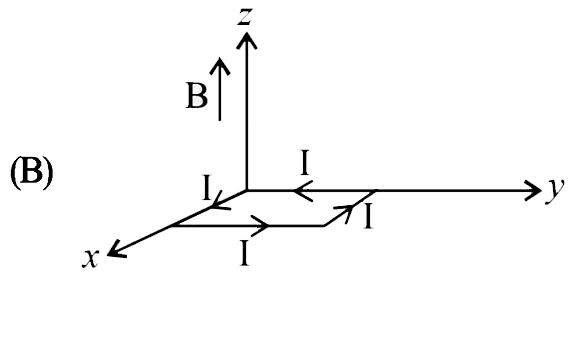

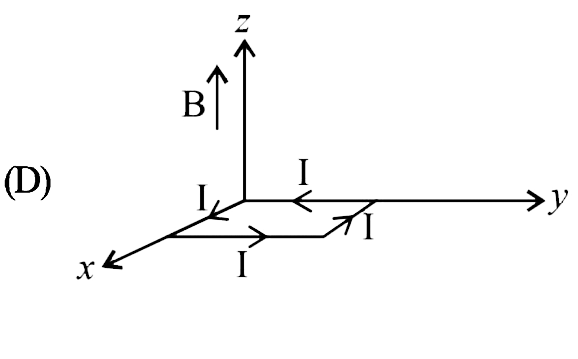
View SolutionIn which orientation, a dipole placed in a uniform electric field is in (i) stable (ii) unstable equilibrium ?
View SolutionSome metals get magnetised by orientation of atomic magnetic moments in external magnetic field. What are they called?
View Solution
