Zदिशा के अनुदिश गतिमान एक समतल वैधुतचुमबकीय तरंग को E=E0sin(kz–εt)ˆIतथाB=B0sin(kz–εt)ˆj द्वारा वर्णित किया गया है। दर्शाइए कि
(i) तरंग का औसत ऊर्जा घनत्व है।
μav=14E0E20+14.B20μ0
(ii) तरंग की काल – ओसत तीव्रता है।
Iav=12CE0E20
(i) Eक्षेत्र का येागदार हैं EE=12ε0E2
B=क्षेत्र का योगदान है μB=12.B2μ0
कुल ऊर्जा घनत्व μ=μE+μB=12ε0E2+12.B2μ0
E2 तथाB2 के मान प्रत्येक बिन्दु तथा प्रत्येक क्षण पर परिवर्ती होते हैं अत:E∘तथाB2 के प्रभावी मान उनके कालिक मान है।
(B−2)ε=E20[sin2(kz−εt)]ε
sin2θ तथाcos2θ के ग्राफ आकृति में समरूप है लेकिन π/2 से स्थानान्तरित है। अतsin2θ तथाcos2θ के औसत मान भी π के किसी पूर्ण संख्यिकी गुणज के लिए समान है।
तथाsin2θ+cos2θ=
अत:सममिति से sin2θ का औसत =cos2θ का औसत =12
(E2)ε=12E∘0“and“(B2)ε=12B20
समीकरण 1 में प्रस्थान करने पर
μ=14ε0E2+14B20μ
(ii) इमें ज्ञात है। E0B0=c तथाc=1√μ0ε0∴,14.B204μ0=E204μ0μ0ε0=14ε0E20
με=14ε0E20+14ε0=12ε0E20तथाIε=μεc=12ε0E20
Topper's Solved these Questions
Similar Questions
सोडियम के किसी तनु लक्ष्य (10−2m2 क्षेत्रफल, 10−3m मोटाई) पर विचार कीजिए जिस पर जब 100W/m2 तीव्रता का प्रकाश (λ=660nm) डाला जाता है तो इससे 100μA की प्रकाश विद्युत धारा उत्पन्न होती है। जब कोई इलेक्ट्रॉन किसी सोडियम परमाणु (Na का घनत्व 0.97kg/m3) से टकराता है तो फोटोइलेक्ट्रॉन उत्पन्न होने की प्राथमिकता परिकलित कीजिए।
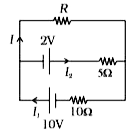
03:36View Solutionदो सेल जिनकी वोल्टता 10Ω तथा 2V एवं आन्तरिक प्रतिरोध क्रमश: 10Ω तथा 5Ω हैं, पार्श्वक्रम में इस प्रकार संयोजित हैं कि 10v बैटरी का धनात्मक टर्मिनल 2V बैटरी के ऋणात्मक टर्मिनल से संयोजित है (चित्र 3.8)। संयोजन की प्रभावी वोल्टता तथा प्रभावी प्रतिरोध ज्ञात कीजिए।
 01:50View Solution
01:50View SolutionElectric field strength bar(E)=E_(0)hat(i) and bar(B)=B_(0)hat(i) exists in a region. A charge is projected with a velocity bar(v)=v_(0)hat(j) at origin , then
03:53View Solutionif E=E_(0)sin(kz-omegat) and B=B_(0)(kz-omegat) are electric and magnetic field produced by an electromagnetic wave travelling in +z direction in a medium. Then if eta=(E_(0))/(B_(0)) , then the value of eta is [mu =permeability of a medium epsilon= permittivity of medium]
08:55View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0ˆk. Total electric flux passing through the cube would be
03:14View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E_(0) " sin "(kz- omegat) hati " and " B =B_(0) " sin " (kz- omegat) hatj (i) Evaluate intE. dl over the rectangular loop 1234 shown in figure. (ii) Evaluate int B.ds over the surface bounded by loop 1234. (iii) Use equation int E.dl = (-dphi_(B))/(dt) to prove (E_(0))/(B_(0)) =c. (iv) By using similar proces and the equation int B.dl =mu_(0) I+ epsilon_(0) (dphi_(E))/(dt), prove that c (1)/(sqrt(mu_(0) epsilon_(0))
02:48View SolutionThe magnetic field of a plane electromagnetic wave is given by: →B=B0ˆi−[cos(kz−ωt)]+B1ˆjcos(kz+ωt) where B0=3×10−5T and B1=2×10−6T. The rms value of the force experienced by a stationary charge Q=10−4C at z=0 is close to:
03:06View SolutionAn electromagnetic wave travels in vacuum along z - direction : →E=(E1ˆi+E2ˆj)cos(kz−ωt). Choose the correct options from the following :
05:00View SolutionA plane EM wave travelling in vacuum along z - direction is given by →E=E0sin(kz−ωt)ˆi and →B=B0sin(kz−ωt)ˆj.
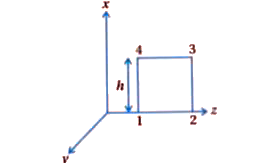
Use equation ∫→E.→dl=−dϕBdt to prove E0B0=c.02:19View SolutionA plane EM wave travelling in vacuum along z - direction is given by vec(E )=E_(0)sin (kz - omega t)hat(i) and vec(B)=B_(0)sin(kz - omega t)hat(j) . By using similar process and the equation int vec(B).vec(d)l = mu_(0)I+ in_(0)(d phi_(E ))/(dt) , prove that c=(1)/(sqrt(mu_(0)in_(0)))
01:48View SolutionA plane EM wave travelling along z - direction is desctribed vec(E )=E_(0)sin(kz - omega t)hat(i) and veC(B)=B_(0)sin (kz - omega)hat(j) . Show that The average energy density of the wave is given by U_(av)=(1)/(4)in_(0)E_(0)^(2)+(1)/(4).(B_(0)^(2))/(mu_(0)) .
13:58View SolutionA plane EM wave travelling along z - direction is desctribed →E=E0sin(kz−ωt)ˆi and veC(B)=B0sin(kz−ω)ˆj. Show that
The time averaged intensity of the wave is given by Iav=12c∈0E20.04:35View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E_(0) " sin "(kz- omegat) hati " and " B =B_(0) " sin " (kz- omegat) hatj (i) Evaluate intE. dl over the rectangular loop 1234 shown in figure. (ii) Evaluate int B.ds over the surface bounded by loop 1234. (iii) Use equation int E.dl = (-dphi_(B))/(dt) to prove (E_(0))/(B_(0)) =c. (iv) By using similar proces and the equation int B.dl =mu_(0) I+ epsilon_(0) (dphi_(E))/(dt), prove that c (1)/(sqrt(mu_(0) epsilon_(0))
View SolutionThe magnetic field of a plane electromagnetic wave is given by: →B=B0ˆi−[cos(kz−ωt)]+B1ˆjcos(kz+ωt) where B0=3×10−5T and B1=2×10−6T. The rms value of the force experienced by a stationary charge Q=10−4C at z=0 is close to:
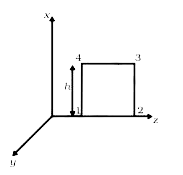
03:38View Solutionनिर्वात में z दिशा के अनुदिश गमनशील एक समतल वैधुतचुबकीय तरंग को E=E0sin(kz−εt)ˆI तथा B=B0sin(kz−εt)ˆj द्वारा प्रदर्शित किया गया हैं
(i)चित्र में दर्शाइए गए आयताकार लूप 1234 पर ∫E.d1 का मान ज्ञात कीजिए
(ii) लूप 1234 द्वारा घिरे पुष्ठ के लिए ∫B.ds का मान ज्ञात कीजिए।
(iii) समीकरण ∫E.d1=−dϕBdt का उपयोग करके सिध्द कीजिए E0B0=c
(iv) इसी प्रकार की प्रकिया तथा समीकरण OB.d1=μ0I+E0dϕEdt का उपयोग करके सिध्द कीजिए कि c=1√μ0E0
 View Solution
View Solution

