Each side of ΔABC is the polarof the opposite vertex with respect to a circle with centre P. For the ΔABC the point P is
centroid
circum centre
incentre
ortho centre
The correct Answer is:D
To solve the problem, we need to show that the point P is the circumcenter of triangle ΔABC when each side of the triangle is the polar of the opposite vertex with respect to a circle centered at P.
1. Understanding the Concept of Polar and Vertex:
- The polar of a point with respect to a circle is the line that represents all points from which the tangents to the circle from that point are equal in length. In this case, each side of triangle ΔABC is the polar of the opposite vertex.
2. Drawing the Triangle and Circle:
- Draw triangle ΔABC with vertices A, B, and C.
- Mark point P as the center of the circle. Draw the circle with center P that intersects the triangle.
3. Identifying the Polars:
- Identify the sides of the triangle:
- Side BC is the polar of vertex A.
- Side CA is the polar of vertex B.
- Side AB is the polar of vertex C.
4. Using the Property of Polars:
- Since each side of the triangle is the polar of the opposite vertex, we can conclude that the distances from point P to each side of the triangle are equal. This is a property of the circumcenter.
5. Conclusion:
- Since P is equidistant from all three sides of triangle ΔABC, it follows that P is the circumcenter of the triangle. Therefore, the point P is the circumcenter of triangle ΔABC.
Final Statement:
Thus, we conclude that the point P is the circumcenter of triangle ΔABC.
---
- The polar of a point with respect to a circle is the line that represents all points from which the tangents to the circle from that point are equal in length. In this case, each side of triangle ΔABC is the polar of the opposite vertex.
- Draw triangle ΔABC with vertices A, B, and C.
- Mark point P as the center of the circle. Draw the circle with center P that intersects the triangle.
- Identify the sides of the triangle:
- Side BC is the polar of vertex A.
- Side CA is the polar of vertex B.
- Side AB is the polar of vertex C.
- Since each side of the triangle is the polar of the opposite vertex, we can conclude that the distances from point P to each side of the triangle are equal. This is a property of the circumcenter.
- Since P is equidistant from all three sides of triangle ΔABC, it follows that P is the circumcenter of the triangle. Therefore, the point P is the circumcenter of triangle ΔABC.
Thus, we conclude that the point P is the circumcenter of triangle ΔABC.
Similar Questions
Each side of ΔABC is the polar of the opposite vertex with respect to a circle with centre P. Then P is ortho centre of ΔABC.
View SolutionLet the equations of perpendicular bisectors of sides ACandABofΔABCisx+y=3andx−y=1 respectively Then vertex A is is (0,0)
The circumcentre of the ΔABC is
View SolutionIf the quadratic equation ax2+bx+c=0 has equal roots where a, b, c denotes the lengths of the sides opposite to vertex A, B and C of the ΔABC respectively then find the number of integers in the range of sinAsinC+sinCsinA
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then (a) the area of ΔABC is maximum when it is isosceles (b) the area of ΔABC is minimum when it is isosceles (c) the perimeter of ΔABC is minimum when it is isosceles (d) none of these
View SolutionDraw a circle of radius 4 cm. Take a point P on it. Without using the centre of the circle, draw a tangent to the circle at point P .
View SolutionIn the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
View SolutionDraw a circle of radius 3 cm. Take a point P outside it. Without using the centre of the circle, draw two tangents to the circle from the point P.
View SolutionDraw a circle of radius 3 cm and take a point P outside it. Without using the centre of the circle draw two tangents of the circle from the point P.
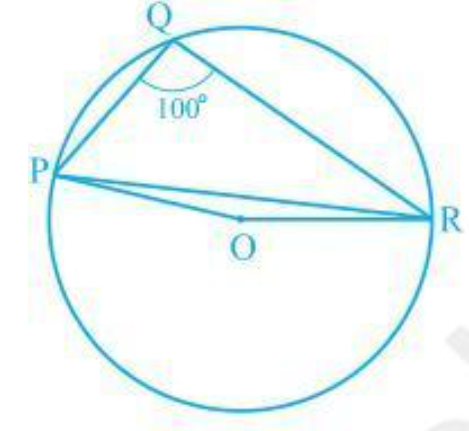
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
View SolutionIf the sum of squares of two sides is equal to square of third side then ΔABC is
View Solution