Two chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB. Show that l bisects CD
Video Solution
Text Solution
We know that the perpendicular bisector of any chord of a circle always passes through its centre.
Since l is the perpendicular bisector of AB, l passes through the centre O of the circle.
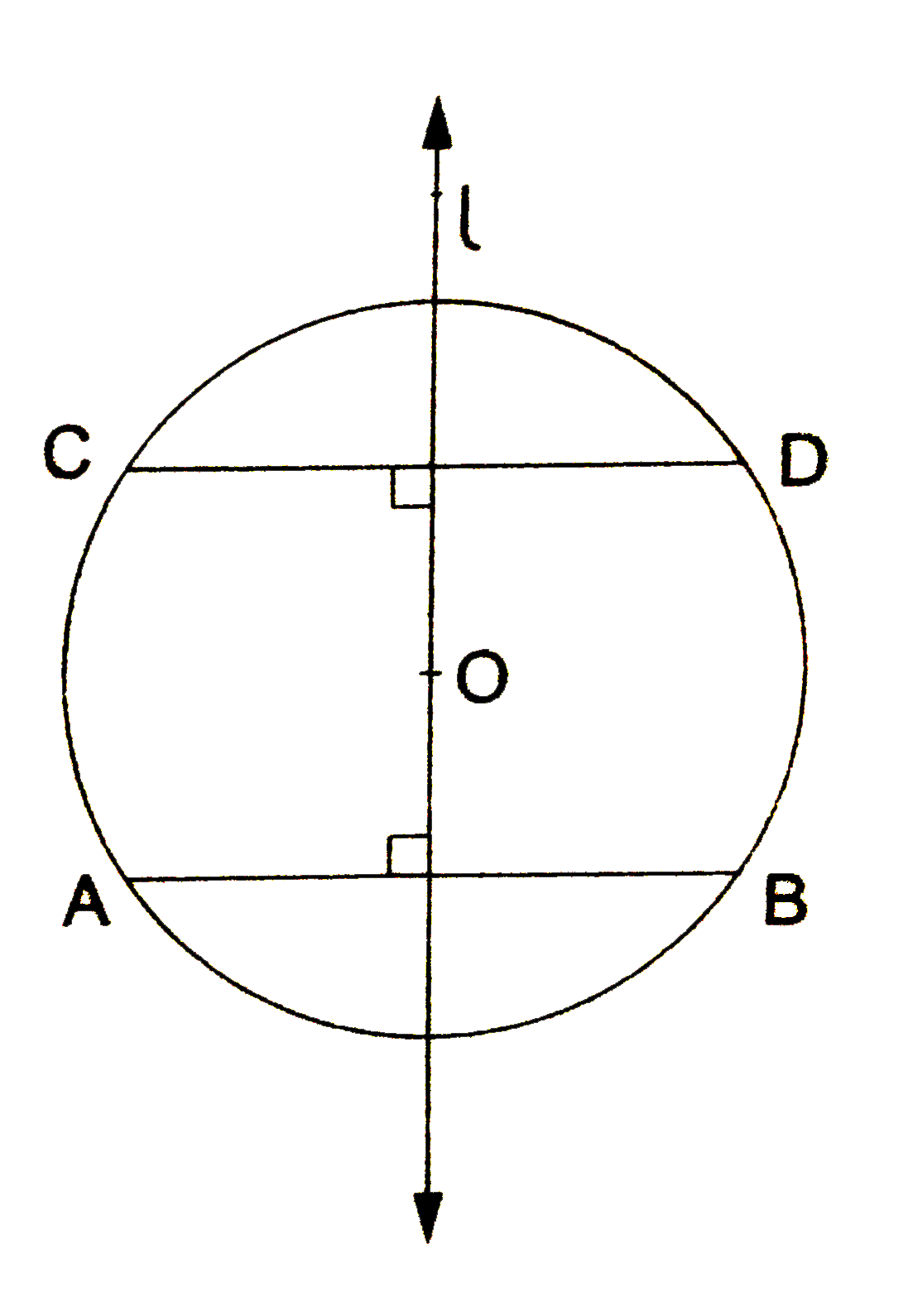
Now, l⊥ AB and AB∣∣CD⇒l⊥CD
Thus, l⊥CD and passes through the centre of the circle.
But, the perpendicular from the centre ofa circle to a chords bisects the chord.
∴ l must bisect the chord CD.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
Two particles each of mass 'm' are placed at A and C are such AB=BC=L. The gravitational force on the third particle placed at D at a distance L on the perpendicular bisector of the line AC is
AGm2L2 along BDBGm2√2L2 along DBCGm2L2 along ACDGm2√2L2 along BD - Question 2 - Select One
Observe the following facts for a parabola.
(i) Axis of the parabola is the only line which can be the perpendicular bisector of the two chords of the parabola.
(ii) If AB and CD are two parallel chords of the parabola and the normals at A and B intersect at P and the normals at C and D intersect at Q, then PQ is a normal to the parabola.
For the parabola y2=4x, AB and CD are any two parallel chords having slope 1. C1 is a circle passing through O, A and B and C2 is a circle passing through O, C and D. C1andC2 intersect atA(4, -4)B(-4, 4)C(4, 4)D(-4, -4) - Question 3 - Select One
Observe the following facts for a parabola.
(i) Axis of the parabola is the only line which can be the perpendicular bisector of the two chords of the parabola.
(ii) If AB and CD are two parallel chords of the parabola and the normals at A and B intersect at P and the normals at C and D intersect at Q, then PQ is a normal to the parabola.
The directrix of the parabola isAy−124=0By+124=0Cy+112=0Dy−112=0
AB is a line segment and line l is its perpendicular bisector. If a point P lies on l, show that P is equidistant from A and B.
View SolutionTheorem :-2 The perpendicular from centre of a circle to the chord bisects the chord and Perpendicular bisectors of two chords of a circle intersects at the centre.
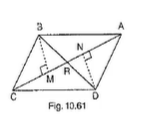
View SolutionIn Figure, BM and DN are both perpendiculars to the segments AC and BM=DN . Prove that AC bisects BD
 View Solution
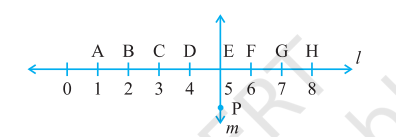
View SolutionStudy the diagram. The line l is perpendicular to line m (a) Is CE=EG (b) Does PE bisect CG = (c) Identify any two line segments for which PE is the perpendicular bisector. (d) Are these true? (i) AC>EG (ii) CD=GH (iii) BC<EH
 View Solution
View SolutionABCD is a parallelogram and line segments AX,CY bisect the angles AandC, respectively. Show that AX∣∣CY
View Solution

