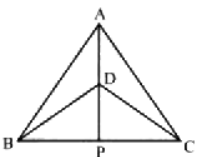
ABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
In △ABD and △ACD,
AB=AC [Since △ABC is isosceles]
AD=AD [common side]
BD=DC [Since △BDC is isosceles]
△ABD≅△ACD [By SSS criteria]
∴∠BAD=∠CAD
⇒∠BAP=∠PAC [By CPCT]
In △ABP and △ACP,
AB=AC [Since △ABC is isosceles]
AP=AP [common side]
∠BAP=∠PAC [from (i)]
∴△ABP≅△ACP [By SAS criteria]
∴BP=PC [By CPCT] ...(ii)
∠APB=∠APC [By CPCT]
△ABD≅△△ACD
∠BAD=∠CAD [From (i)]
∴AD bisects ∠A
⇒AP bisects ∠A ...(iii)
In △BDP and △CDP,
DP=DP [common]
BP=PC [from (ii)]
BD=CD [since △BDC is isosceles]
△BDP≅△CDP [By SSS criteria]
∴∠BDP=∠CDP [CPCT]
∴DP bisects ∠D
⇒AP bisects ∠D ....(iv)
From equation (iii) and equation (iv), we get:
AP bisects ∠A as well as ∠D.
∠APB+∠APC=180∘ [angles in linear pair]
Also, ∠APB=∠APC [from (ii)]
∴∠APB=∠APC=180∘2=90∘
BP=PC and ∠APB=∠APC=90∘
Hence, AP is perpendicular bisector of BC.
Topper's Solved these Questions
Similar Questions
ABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD≅ACD (ii) ABP≅ACP AP bisects ∠A as well as ∠D AP is perpendicular bisector of BC.
 View Solution
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
 View Solution
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
 View Solution
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
 View Solution
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionTriangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
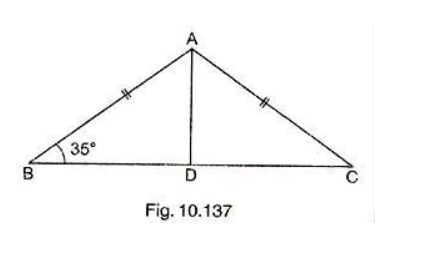
View SolutionABC is an isosceles triangle such that AB=ACandAD is the median to base BC . Then, ∠BAD=
(a) 55∘
(b) 70∘
(c) 35∘
(d) 110∘
 View Solution
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View Solution

