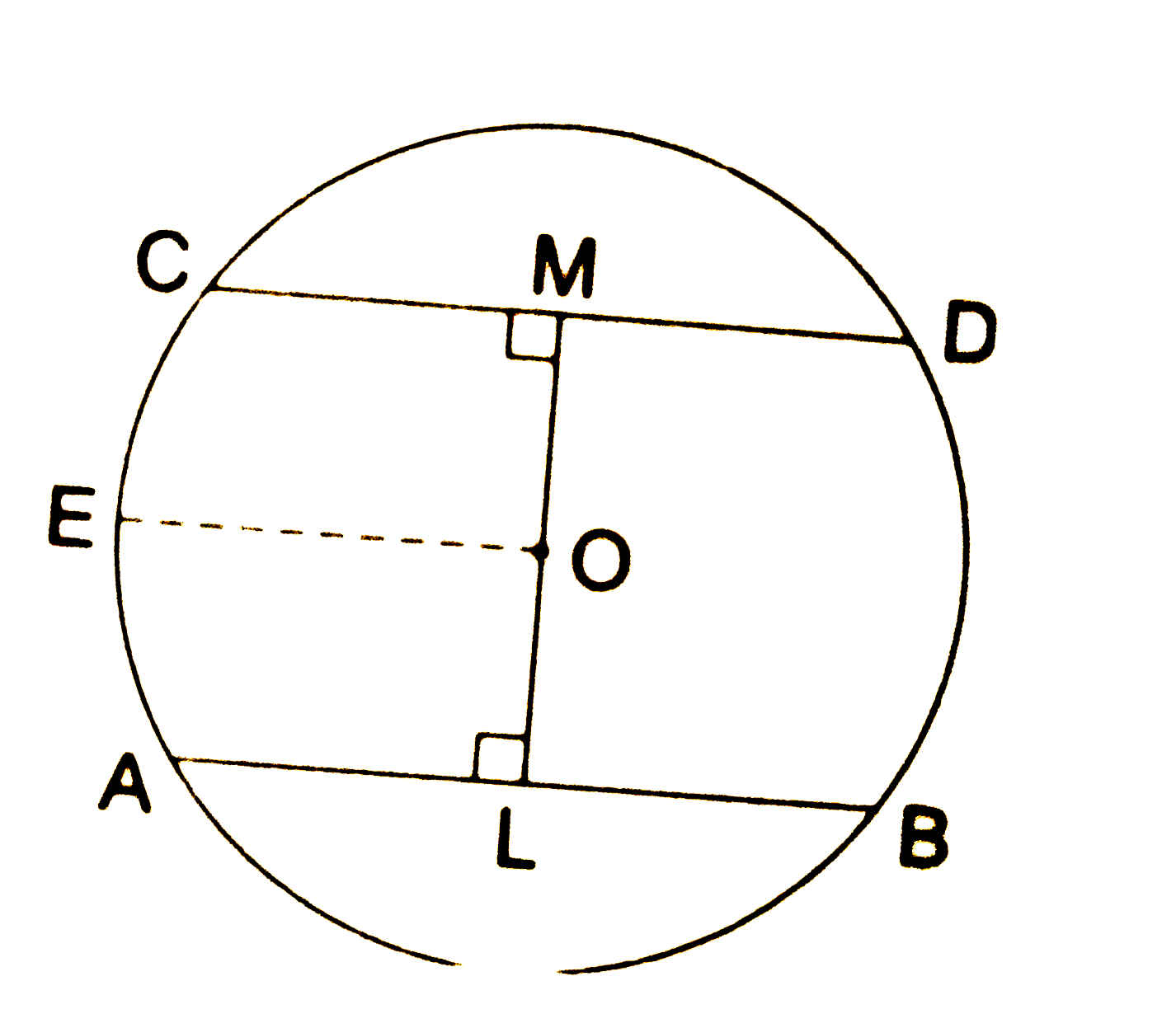
Prove that the line joining the mid-points of two parallel chords of a circle passes through the centre.

Video Solution

Text Solution

Verified by Experts

Given : $L$ and $M$ are midpoints of two parallel chords $A B$ and $C D$ respectively of a circle $C (O, r)$ .
To prove : $L O M$ is a straight line.
Construction : Join $O L, O M$ and draw $O E$ $∣ ∣$ $A B$ $∣ ∣$ $C D$ .
Proof : We know that the line joining the centre of a circle to the midpoint of a chord is perpendicular to the chord.
$∴ O L ⊥ A B$ and $O M ⊥ O E$
Now, $O L ⊥ A B$ and $A B ∣ ∣ O E \Rightarrow O L ⊥ O E$
$\Rightarrow ∠ E O L = 90^{\circ}$
$O M ⊥ C D$ and $C D ∣ ∣ O E \Rightarrow O M ⊥ O E$
$\Rightarrow ∠ E O M = 90^{\circ}$
$∴ ∠ E O L + ∠ E O M = 180^{\circ}$
Hence, $L O M$ is a straight line.

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Similar Questions

Knowledge Check

Question 1 - Select One
The chord of a circle which passes through the centre is___the radius
AThrice
BDouble
CHalf
DEqual to

Recommended Questions

Home
Ask Doubt
Profile