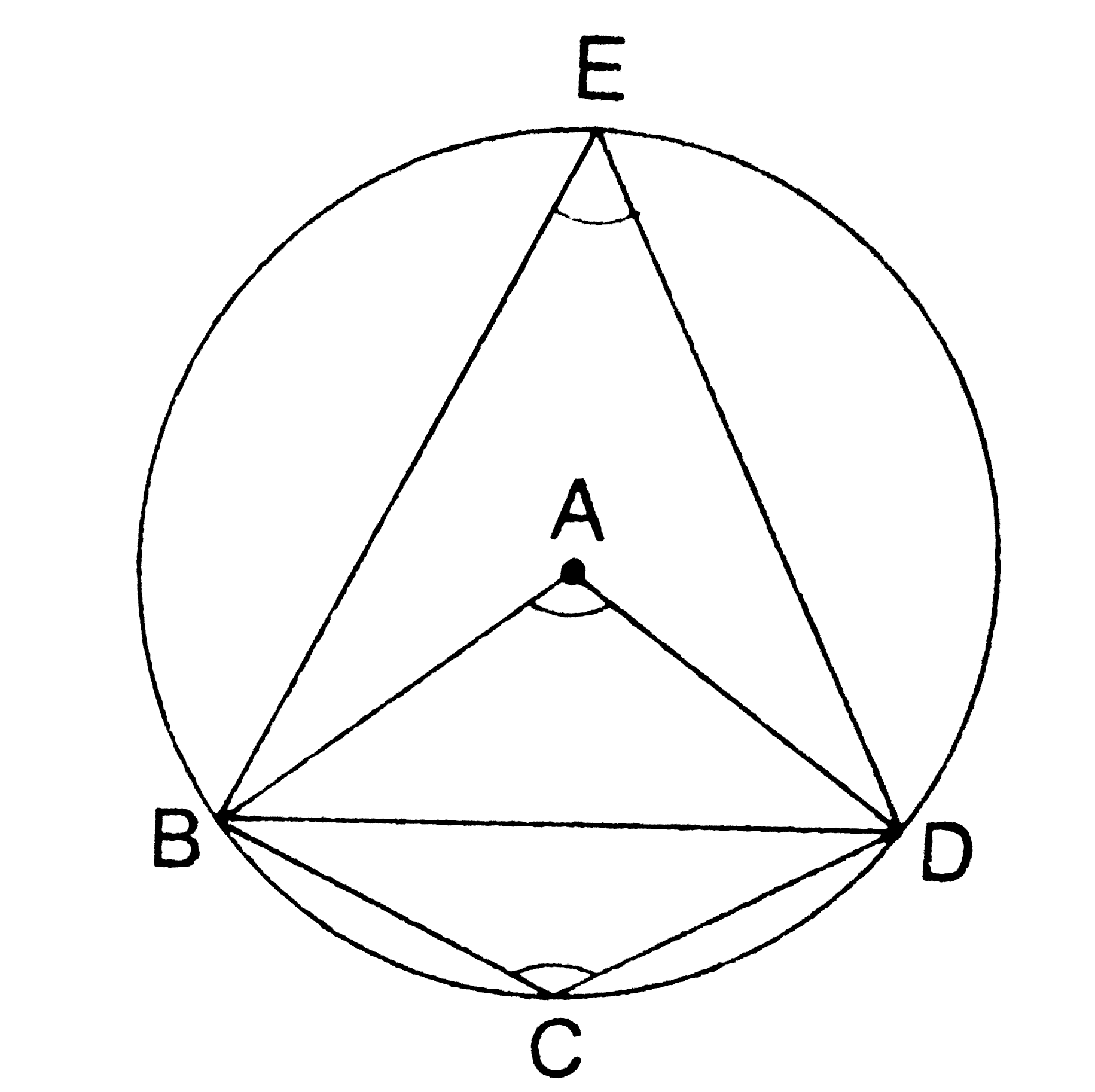
is such a quadrilateral that A is the centre of the circle passing through . Prove that .
Video Solution
Text Solution
With A as centre of AB as radius , draw a circle passing through the points B,C and D.
Take a point E onteh circle outsidearc BCD. Join BE, Deand BD
Clearly, …..(i)
Now, EBCD is a cyclic quadrilateral.
....(ii) [using (i) ]
In , we have
[ using (ii) ].
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
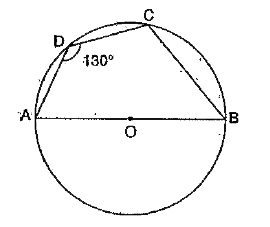
ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If ∠ADC=130∘, find ∠BAC.
 A40∘B50∘C60∘D30∘
A40∘B50∘C60∘D30∘ - Question 2 - Select One
The area of the circle centred at (1,2) and passing through (4,6), is
A5π sq unitsB10π sq unitsC25π sq unitsDNone of these - Question 3 - Select One
The area of circle centred at (1,2) and passing through (4,6) is
A5πB10πC25πDnone of these
In Figure, ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If (∠ADC)=1300, find ∠BAC
View SolutionThe area of the circle centred at (1,2) and passing through (4,6) is
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B).
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B)
View SolutionThe area of circle centred at (1,2) and passing through (4,6) is
View Solution

