In the given figure, l∣∣m and a transversal t cuts them. If ∠7=80∘, find the measure of each of the remaining marked angles.
The correct Answer is:∠1=80∘,∠2=100∘,∠3=80∘,∠4=100∘,∠5=80∘,∠6=100∘,∠8=100∘
To solve the problem step by step, we will use the properties of angles formed by parallel lines and a transversal.
1. Identify Given Information:
- We are given that l∥m (lines l and m are parallel).
- A transversal t intersects these lines.
- The measure of angle 7 is given as 80∘.
2. Find Angle 5:
- Angle 5 is vertically opposite to angle 7.
- By the property of vertically opposite angles, we have:
Angle 5=Angle 7=80∘
3. Find Angle 6:
- Angles 5 and 6 are on a straight line (they form a linear pair).
- The sum of angles on a straight line is 180∘.
- Therefore, we can write:
Angle 6+Angle 5=180∘
- Substituting the value of angle 5:
Angle 6+80∘=180∘
- Solving for angle 6:
Angle 6=180∘−80∘=100∘
4. Find Angle 8:
- Angle 8 is vertically opposite to angle 6.
- By the property of vertically opposite angles, we have:
Angle 8=Angle 6=100∘
5. Find Angle 1:
- Angle 1 is corresponding to angle 5.
- By the property of corresponding angles, we have:
Angle 1=Angle 5=80∘
6. Find Angle 3:
- Angle 3 is vertically opposite to angle 1.
- By the property of vertically opposite angles, we have:
Angle 3=Angle 1=80∘
7. Find Angle 2:
- Angle 2 is corresponding to angle 6.
- By the property of corresponding angles, we have:
Angle 2=Angle 6=100∘
8. Find Angle 4:
- Angle 4 is vertically opposite to angle 2.
- By the property of vertically opposite angles, we have:
Angle 4=Angle 2=100∘
Summary of Angles:
- Angle 1 = 80∘
- Angle 2 = 100∘
- Angle 3 = 80∘
- Angle 4 = 100∘
- Angle 5 = 80∘
- Angle 6 = 100∘
- Angle 7 = 80∘
- Angle 8 = 100∘
- We are given that l∥m (lines l and m are parallel).
- A transversal t intersects these lines.
- The measure of angle 7 is given as 80∘.
- Angle 5 is vertically opposite to angle 7.
- By the property of vertically opposite angles, we have:
Angle 5=Angle 7=80∘
- Angles 5 and 6 are on a straight line (they form a linear pair).
- The sum of angles on a straight line is 180∘.
- Therefore, we can write:
Angle 6+Angle 5=180∘
- Substituting the value of angle 5:
Angle 6+80∘=180∘
- Solving for angle 6:
Angle 6=180∘−80∘=100∘
- Angle 8 is vertically opposite to angle 6.
- By the property of vertically opposite angles, we have:
Angle 8=Angle 6=100∘
- Angle 1 is corresponding to angle 5.
- By the property of corresponding angles, we have:
Angle 1=Angle 5=80∘
- Angle 3 is vertically opposite to angle 1.
- By the property of vertically opposite angles, we have:
Angle 3=Angle 1=80∘
- Angle 2 is corresponding to angle 6.
- By the property of corresponding angles, we have:
Angle 2=Angle 6=100∘
- Angle 4 is vertically opposite to angle 2.
- By the property of vertically opposite angles, we have:
Angle 4=Angle 2=100∘
- Angle 1 = 80∘
- Angle 2 = 100∘
- Angle 3 = 80∘
- Angle 4 = 100∘
- Angle 5 = 80∘
- Angle 6 = 100∘
- Angle 7 = 80∘
- Angle 8 = 100∘
Topper's Solved these Questions
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Multiple Choice Questions (Mcq)
28 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7B
16 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)
24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)
18 Videos
Similar Questions
In the given figure, l∣∣m and a transversal t cuts them. If ∠1=70∘, find the measure of each of the remaining marked angles.
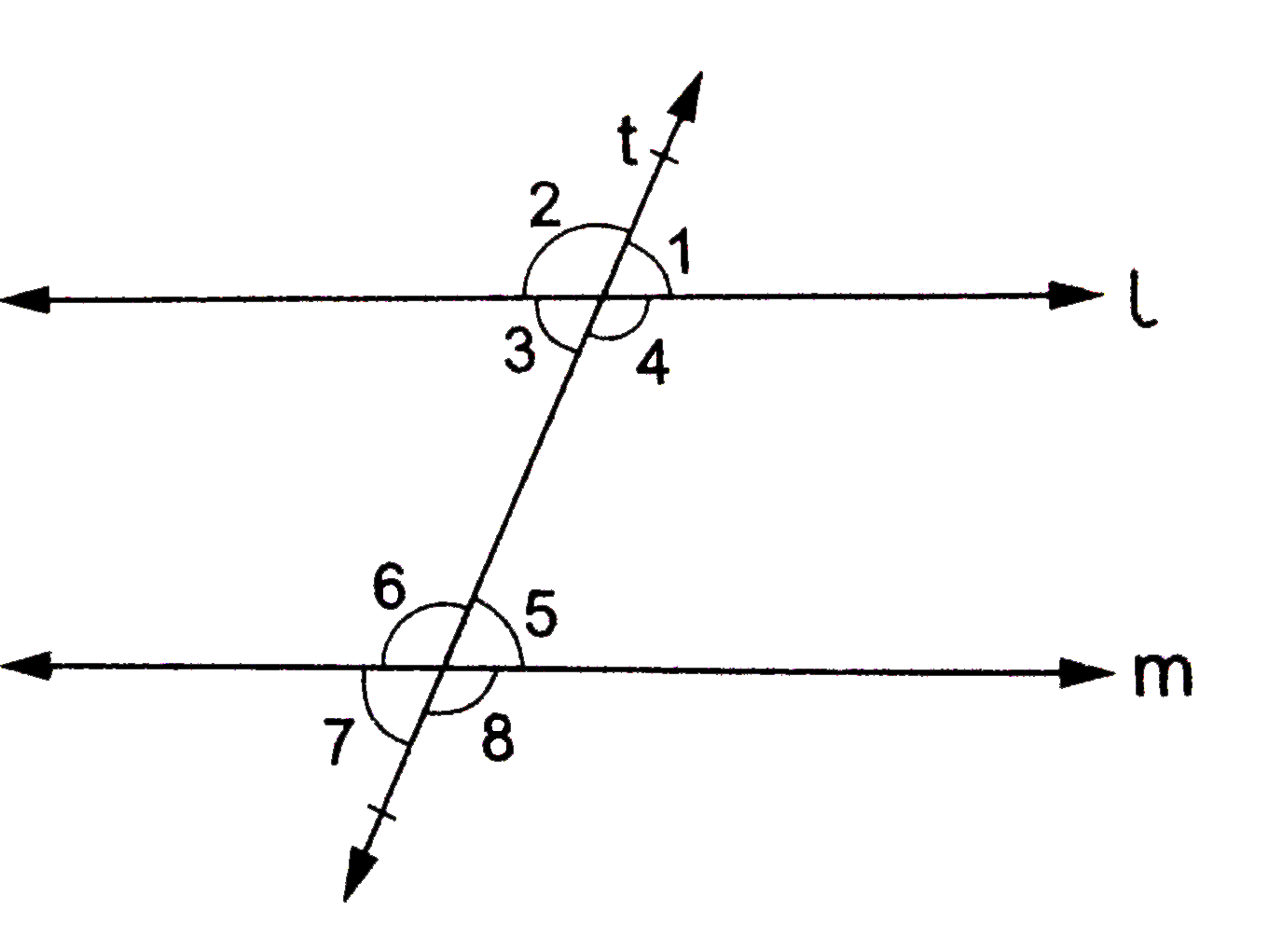
View SolutionIn this given figure, l∣∣m and a transversal t cuts them. If ∠7=120∘, find the measure of each of the remaining marke angles.
View SolutionIn the given figure, l∣∣m and a transversal t cuts them. If ∠1:∠2=5:4, find the measure of each of the marked angles.

View SolutionIn the given figure, l∣∣m and a traversal t cuts them. If ∠1:∠2=2:3, find the measure of each of the marked angles.

View SolutionIn the given figure l||m and n is the transversal , find x.

View SolutionIn the given figure, l∣∣m and t is a transversal. If ∠5=70∘, find the measure of each of the angles ∠1,∠3,∠4 and ∠8.
View SolutionIn the given figure, lllm and t is a transversal. If ∠5=70∘, find the measure of each of the angles ∠1,∠3,∠4and∠8
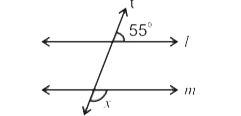
View SolutionIn the given figure if ||m and 't' is the transversal find x .
View SolutionIn the given figure, p ll q and t is the transversal. If ∠1=110∘, find the other angles.
View SolutionIn the given figure l||m and T is a transversal if ∠=70∘ find the measure of the angles ∠1,∠3∠4 and ∠8
View Solution
