Question

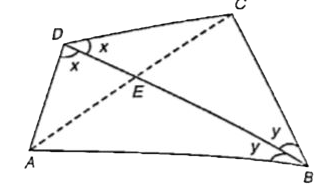
In a quadrilateral ABCD the linesegment bisecting $\angle C\text{and}\angle D$ meet at E. Prove that $\angle A+\angle B=2\angle CED.$

Explanation

Let CE and DE be the bisectors of `angle C and angle D` respectively. Then, `angle 1=(1)/(2) angle C and angle 2 =(1)/(2) angle D.`
In `Delta DEC, " we have " angle 1 + angle 2 + angle CED= 180^(@) ("sum of the " angle " of a " triangle " is " 180^(@))`
`rArr angle CED =180^(@)- (angle 1+angle 2). " " `...(i)
Again, the sum of the angles of a quadrilateral is `360^(@).`
`therefore angle A + angle B +angle C + angle D= 360^(@)`
`rArr (1)/(2) (angle A +angle B)+(1)/(2)angle C+(1)/(2) angle D = 180^(@)`
`rArr (1)/(2)(angle A + angle B)+angle 1+angle 2=180^(@)`
`rArr (1)/(2) (angle A + angle B)=180^(@)-(angle 1+angle 2). " " ` ...(ii)
From (i) and (ii), we get `(1)/(2)(angle A + angle B)=angle CED.`
Hence, `angle A+angle B = 2 angle CED.`