In the adjoining figure, ABCD is a quadrilateral in which AB is the longest side and CD is the shortest side.
Prove that (i) ∠C>∠A, (ii) ∠D>∠B.
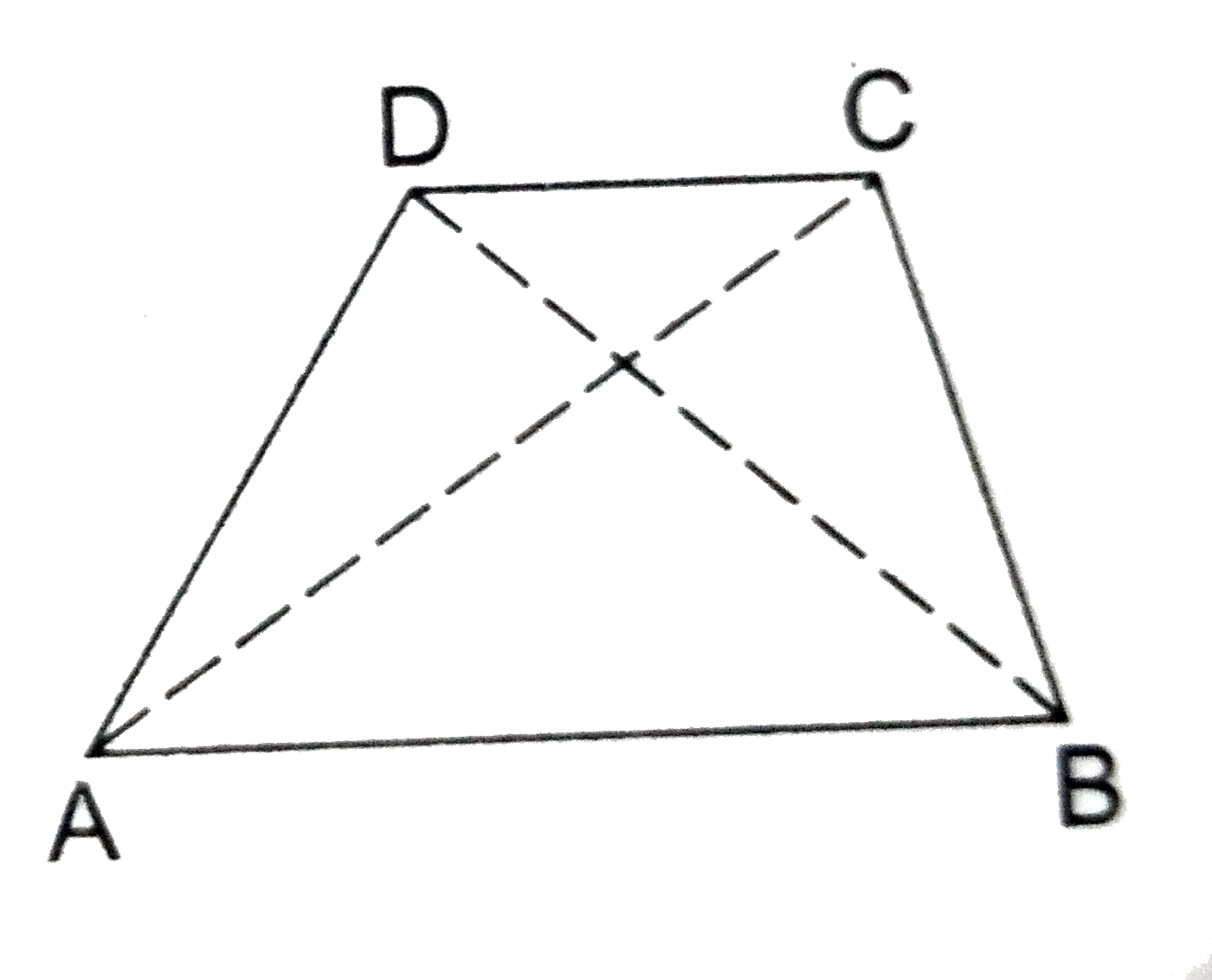
Join AC and BD.
In △ABC,AB>BC⇒∠ACB>∠BAC.
In △ADC,AD>DC⇒∠ACD>∠CAD
[∵ in a triangle, the longer side has the greater angle opposite it].
∴∠ACB+∠ACD>∠BAC+∠CAD.
∴∠C>∠A.
Similarly, ∠D>∠B.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A10videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B27videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
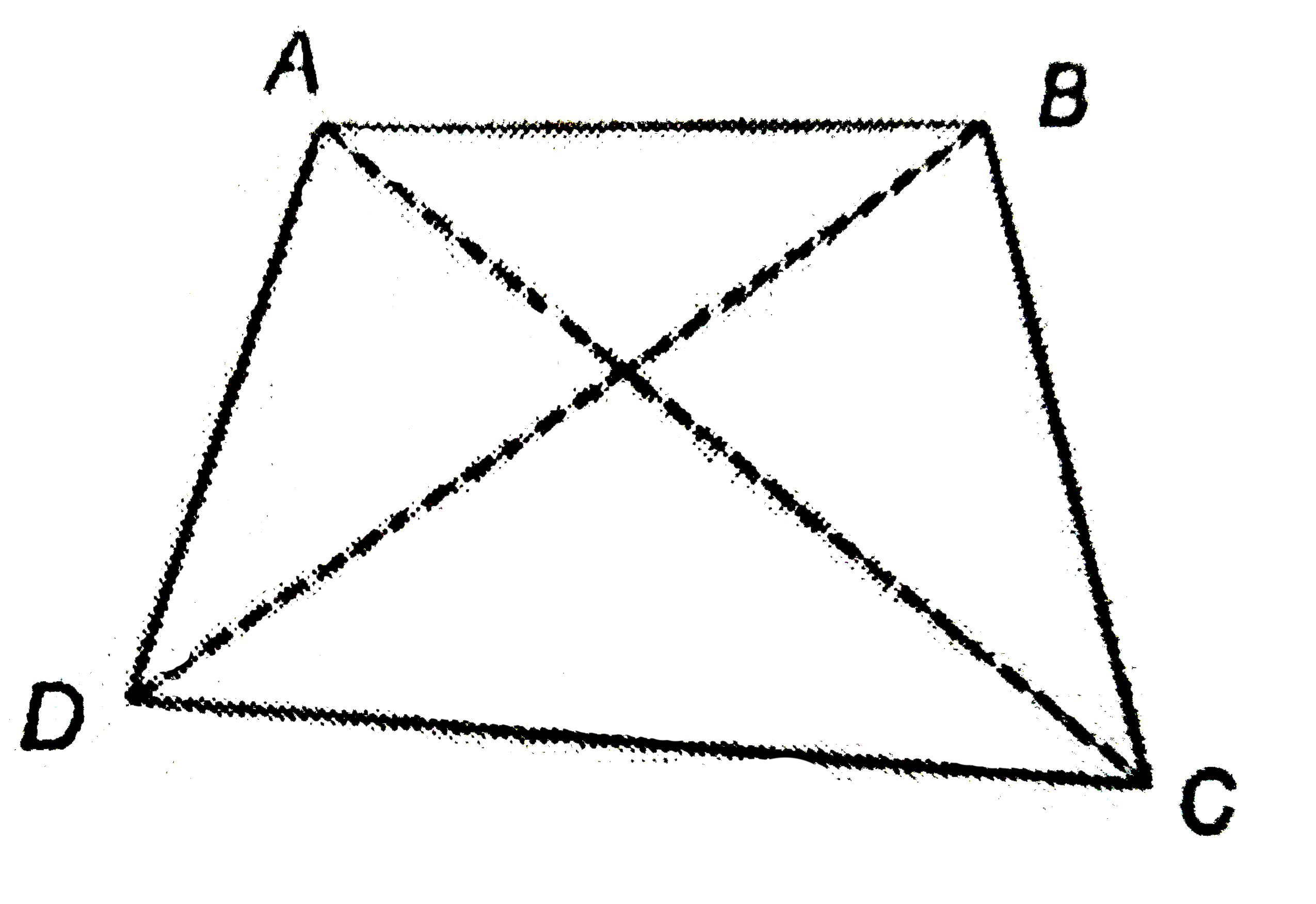
In □ABCD,AB is the smallest and CD is the largest side. Prove that :
(i) ∠B>∠D (ii) ∠A>∠C
 View Solution
View SolutionIn a quadrilateral ABCD, AB is the shortest side and DC is the longest side. What is the relation between
(i) ∠B and ∠D (ii) ∠A and ∠C.View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
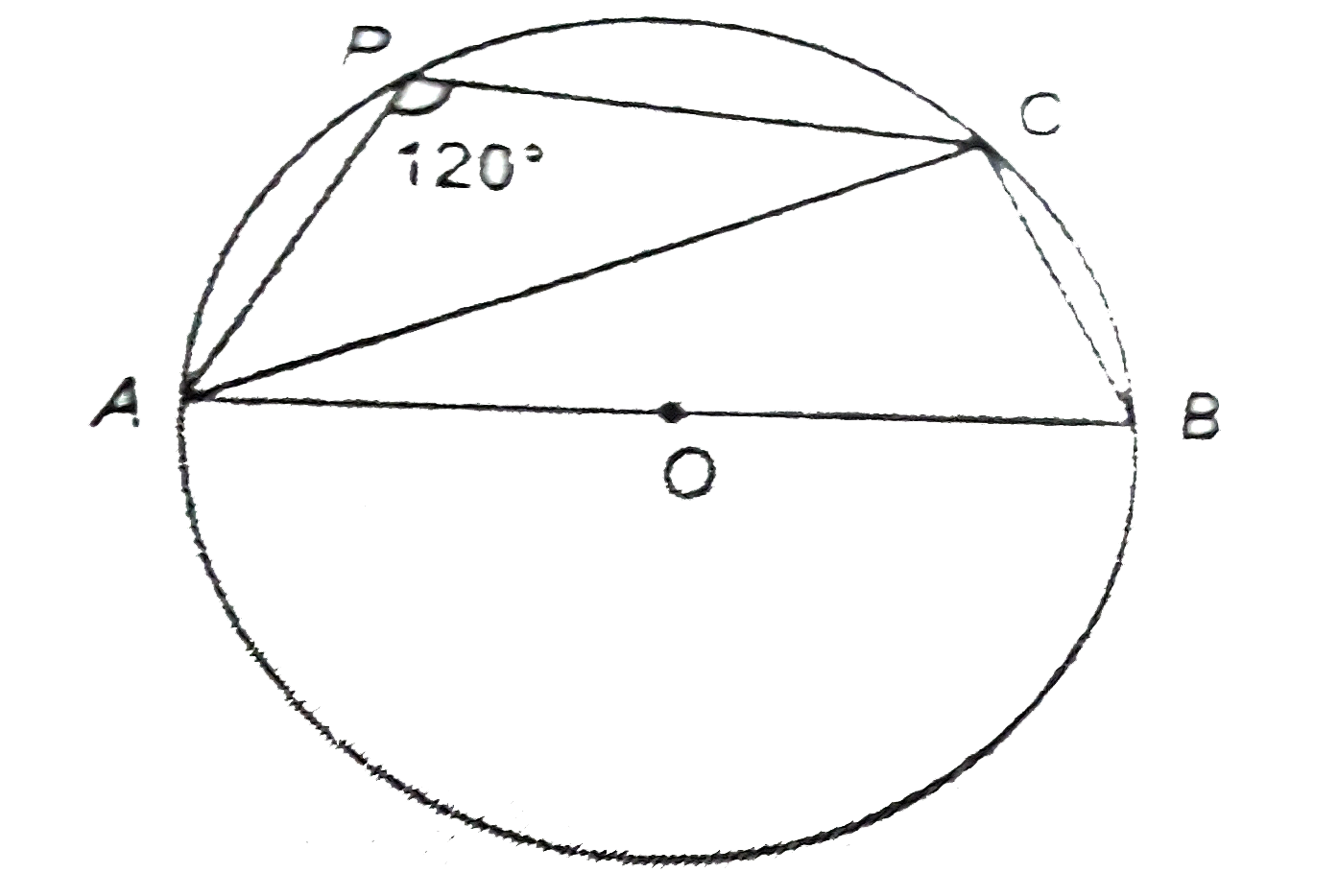 View Solution
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.
 View Solution
View SolutionIn the adjoining figure, ABCD is a rhombus. If ∠A=70∘, find ∠CDB.
 View Solution
View SolutionIn the figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
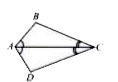 View Solution
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)
 View Solution
View SolutionABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIn the given figure , AC>AB and AD bisects ∠BAC Prove that ∠ADC>ADB
 View Solution
View Solution

