In the adjoining figure, a point O is taken inside an equilateral quad. ABCD such that OB = OD. Show that A, O and C are in the same straight line.
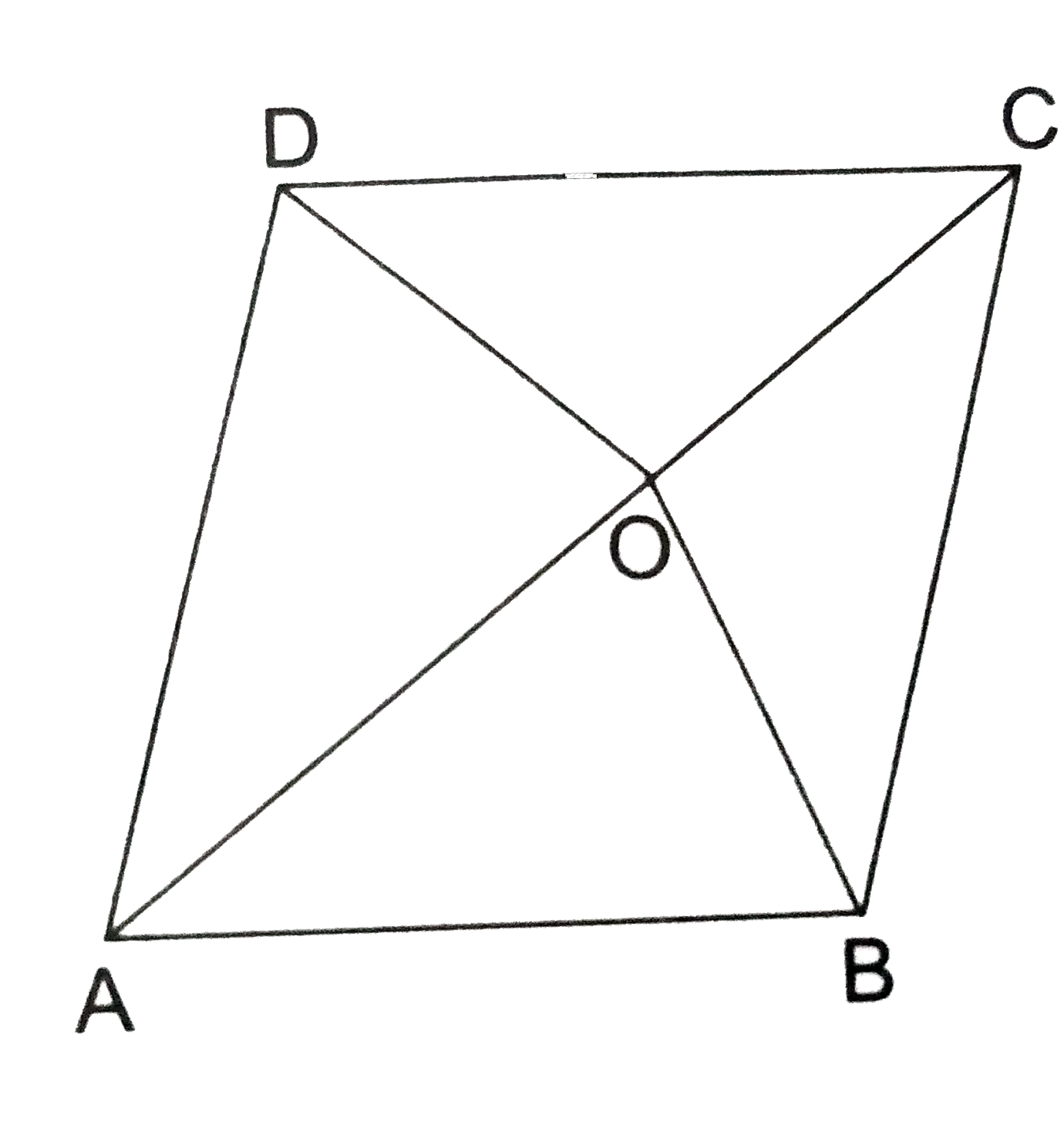
Given A quad. ABCD in which AB = BC = CD = DA and O is a point within it such that OB = OD.
TO PROVE ∠AOB+∠COB=180∘.
PROOF In △OABandOAD, we have
AB = AD (given ), OA = OA (common) and OB = OD (given)
∴△OAB≅△OAD.
∴∠AOB=∠AOD. ...(i)(c.p.c.t.)
Similarly, △OBC≅△ODC.
∴∠COB=∠COD. ...(ii)
Now, ∠AOB+∠COB+∠COD+∠AOD=360∘ [∠ at a point]
⇒2(∠AOB+∠COB)=360∘⇒∠AOB+∠COB=180∘.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A10videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10B27videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Matching of Columns:2videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
A point O is taken inside an equilateral four sided figure ABCD such that its distances from the angular points D and B are equal. Show that AO and OC are in one and the same straight line. GIVEN : A point O inside an equilateral quadrilateral four sided figure ABCD such that BO=OD. TO PROVE : AO and OC are in one and the same straight line.
View SolutionIf O is a point within a quadrilateral ABCD, show that OA+OB+OC+OD>AC+BD.
View Solution
Knowledge Check
- Question 1 - Select One
A point O lies inside a square ABCD such that OA=3, OB=4 and OD=5, find the value of OC.
AA)3√3BB)6.67CC)3√2DD)4√2
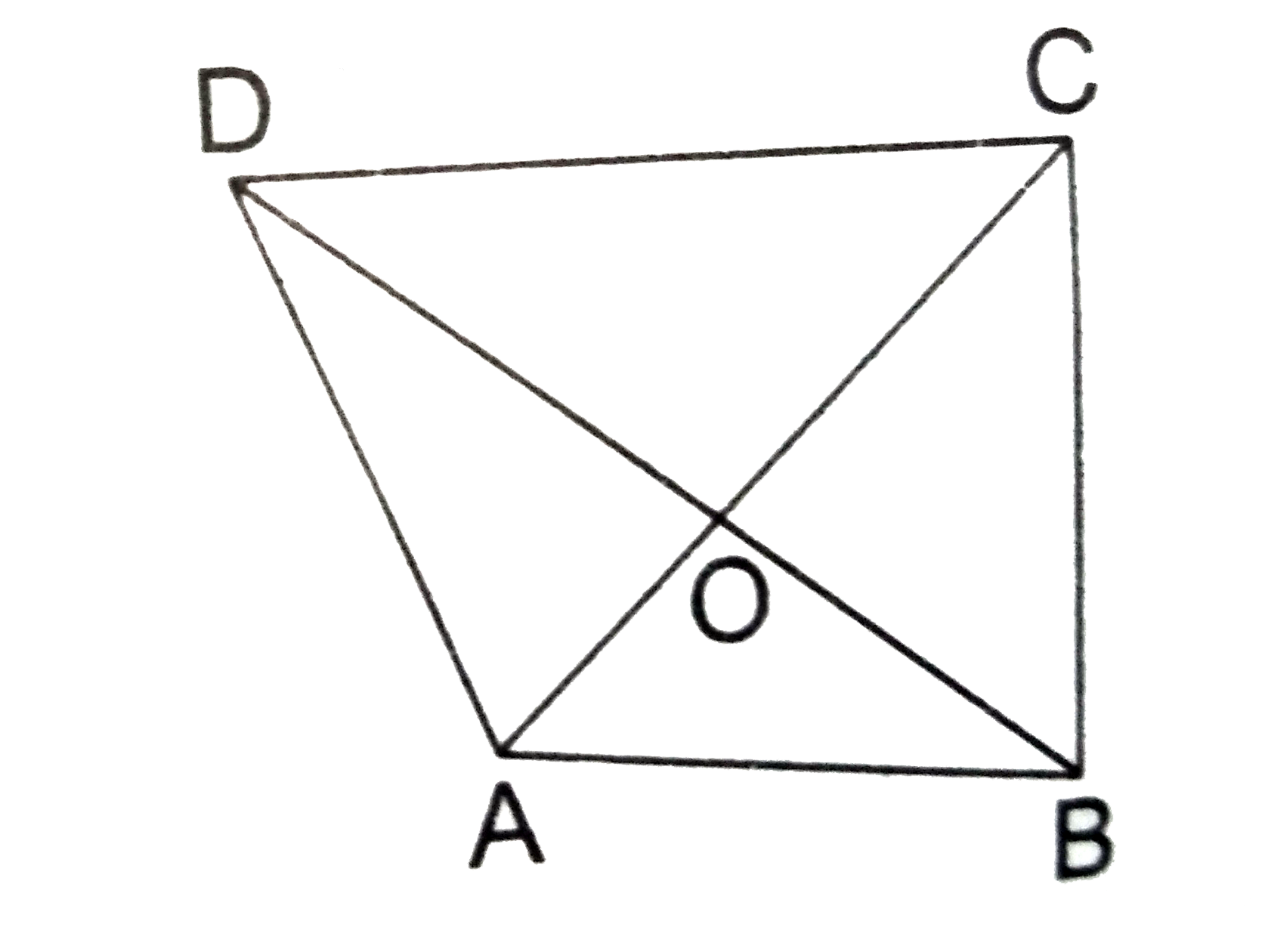
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
 View Solution
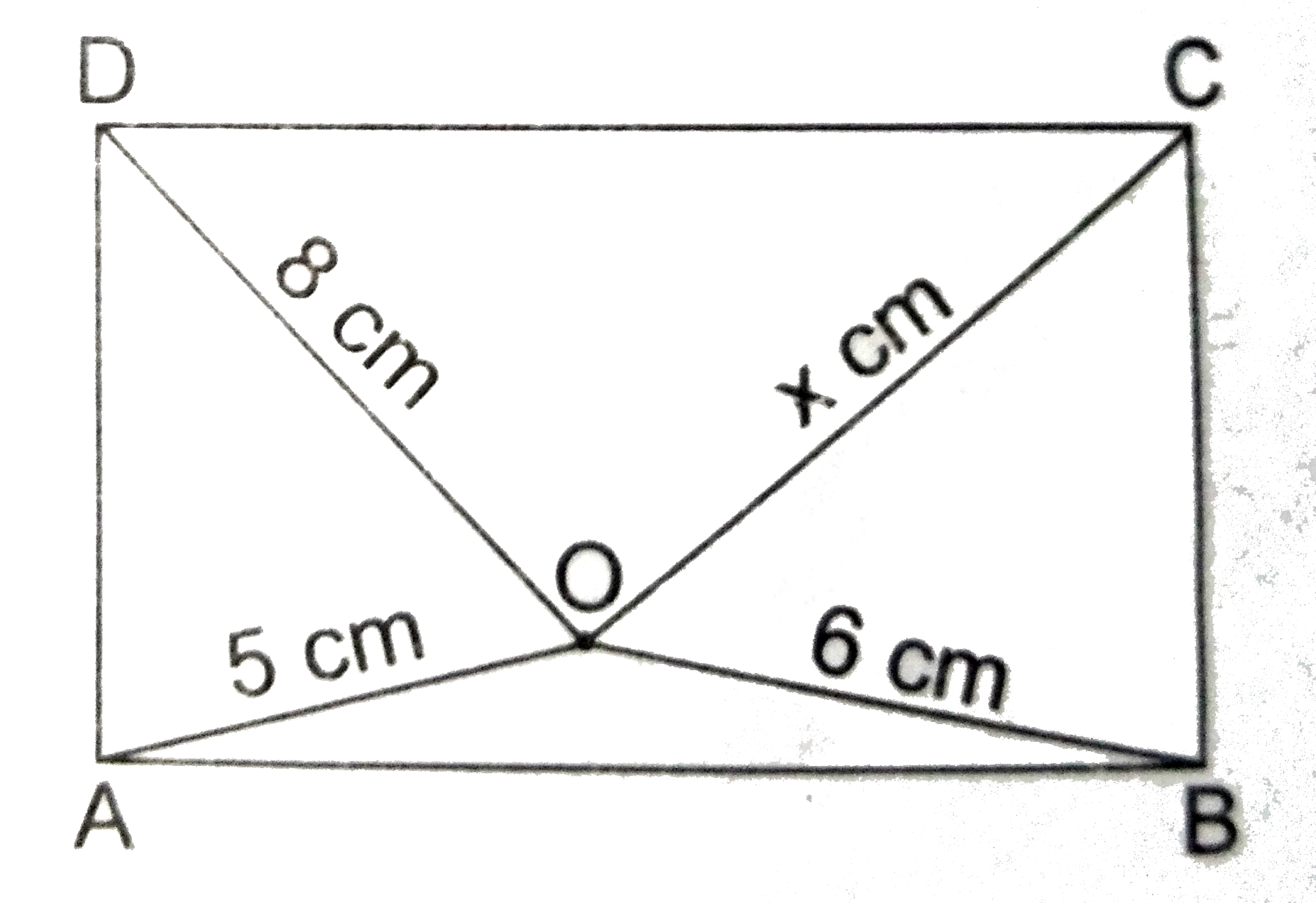
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
 View Solution
View SolutionIn the given figure, ABCD is a square and P is a point inside it such that PB=PD. Prove that CPA is a straight line.
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at 0 such that OB = OD. If AB = CD, then show that

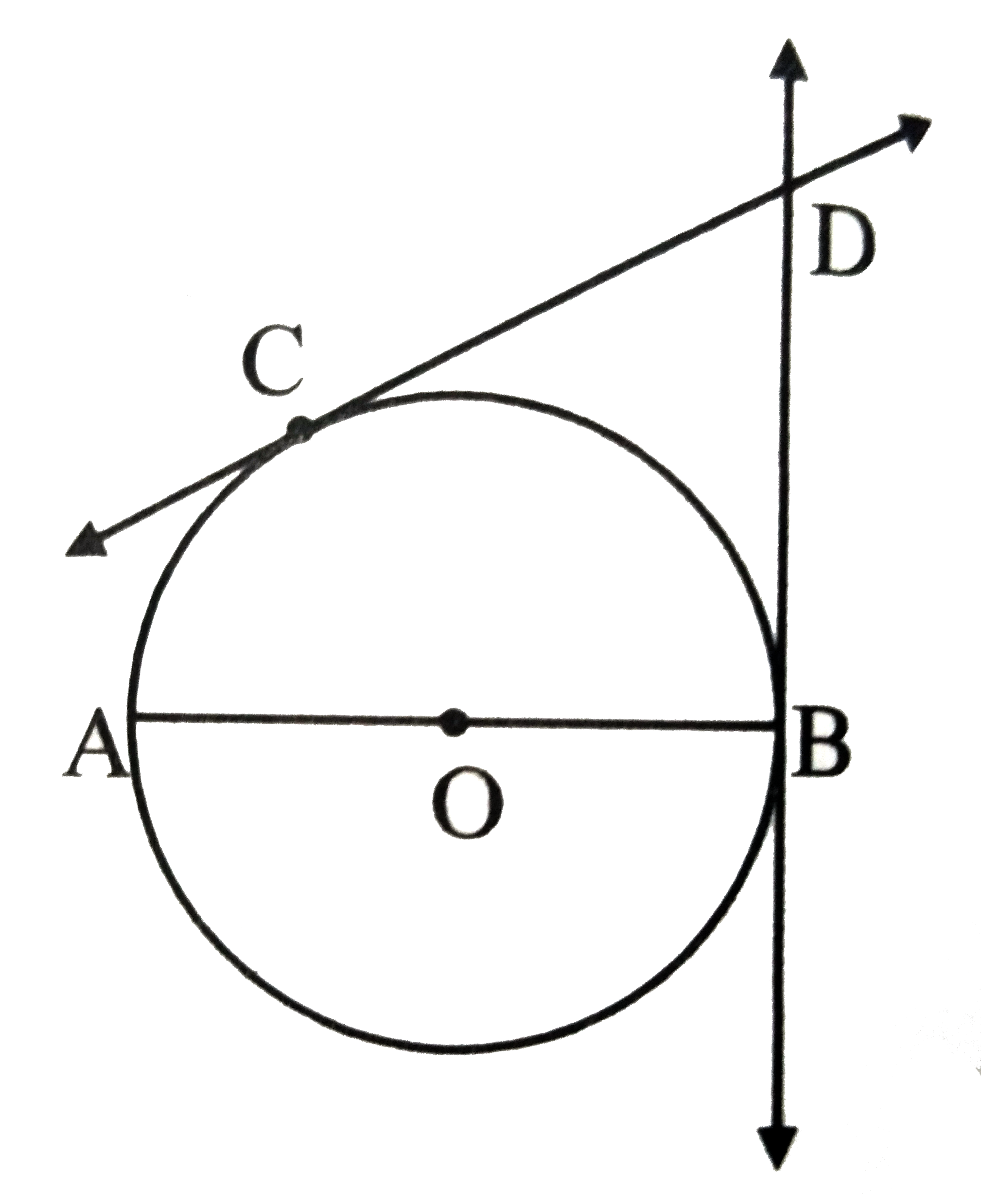
DA I I CB or ABCD is a parallelogram.View SolutionIn the adjoining figure, O is the centre and seg AB is a diameter. At the point C on the circle, the tangent CD is drawn. Line BD is a tangent to the circle at the point B. Show that segOD ∣∣ chord AC.
 View Solution
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)
 View Solution
View SolutionIn the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
View Solution

