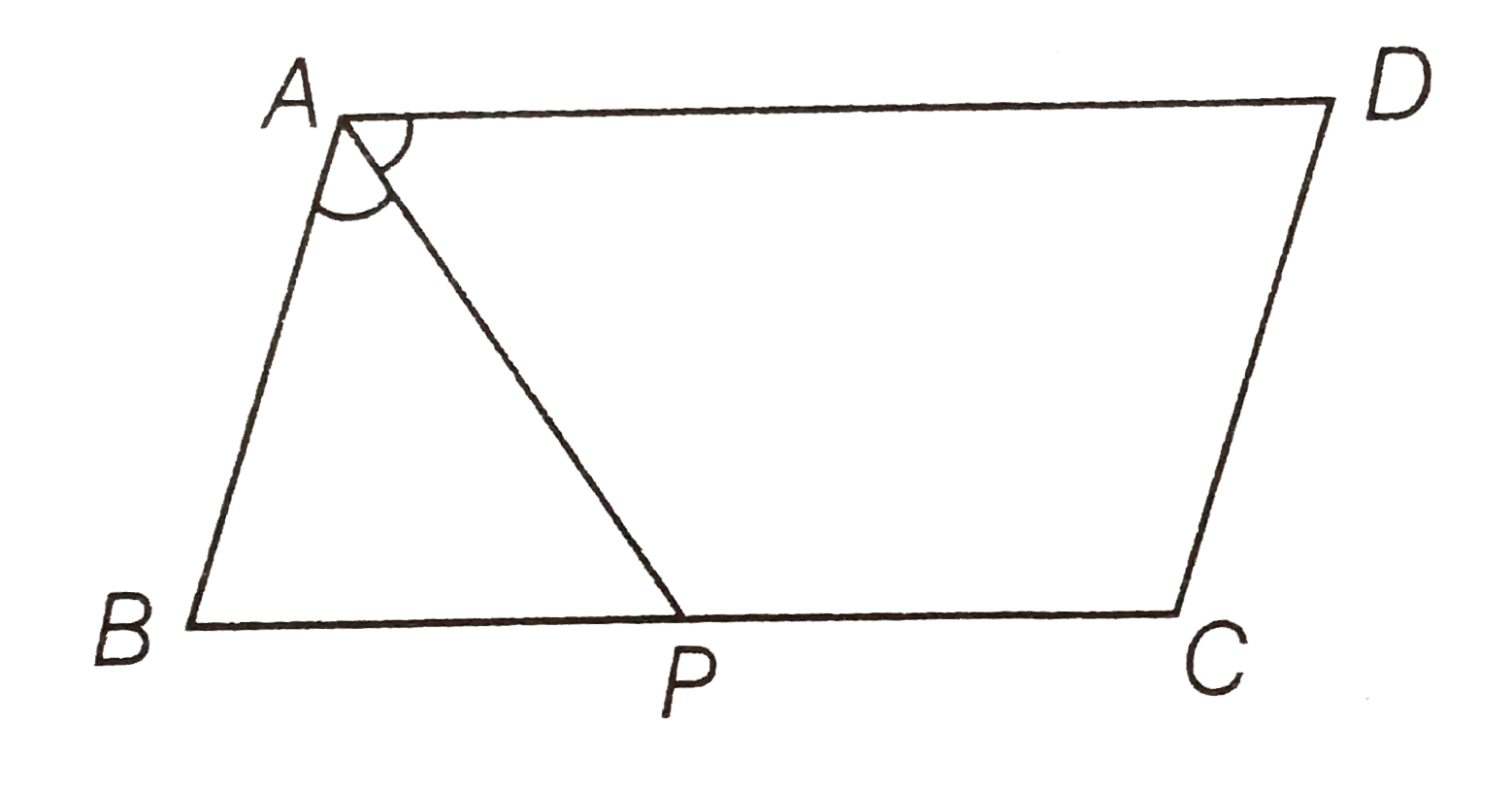
In the adjoining figure, M is the midpoint of side BC of a paralleogram ABCD such that ∠BAM=∠DAM. Prove that AD=2CD.
Video Solution
Text Solution
∠AMB=∠DAM(∵AD||BC)
⇒∠AMB=∠BAM⇒AB=BM⇒CD=12(BC)⇒CD=12(AD)⇒AD=2CD.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 10C18videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)47videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A10videos
QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)16videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)10videos
TRIANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure given below M is the midpoint of side CD of the parallelogram ABCD. What is ON:OB ?
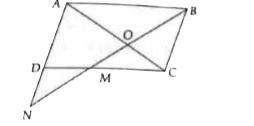 A3:2B2:1C3:1D5:2
A3:2B2:1C3:1D5:2
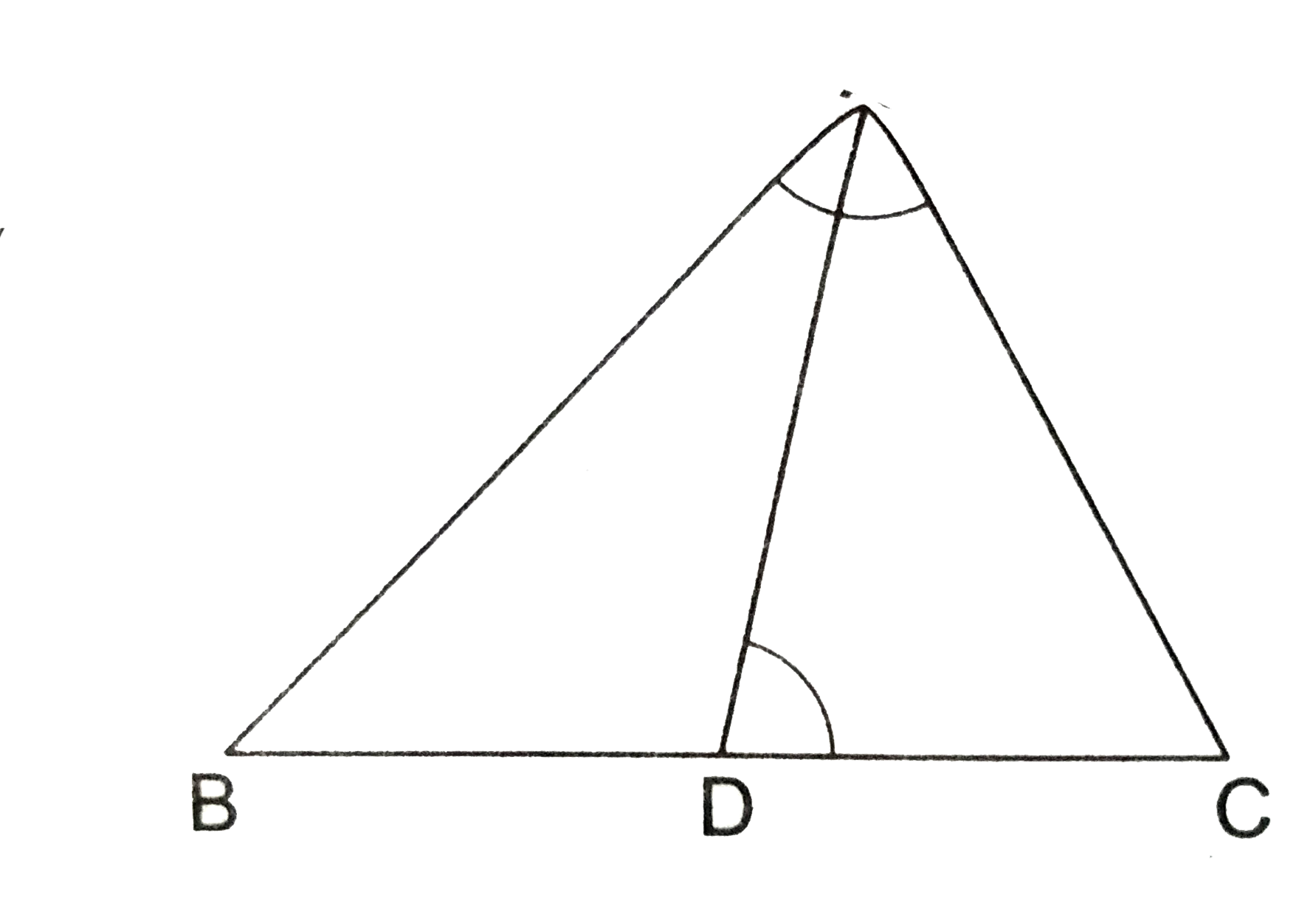
In the given figure , D is a point on the side BC of ΔABC such that ∠ADC=∠BAC. Prove that CA2=CB×CD.
 View Solution
View SolutionIn the given figure. AB∣CDandO is the midpoint of AD.
View SolutionIn the adjoining figure, in ΔABC, point D is on side BC such that, ∠BAC=∠ADC. Prove that, CA2=CB×CD.
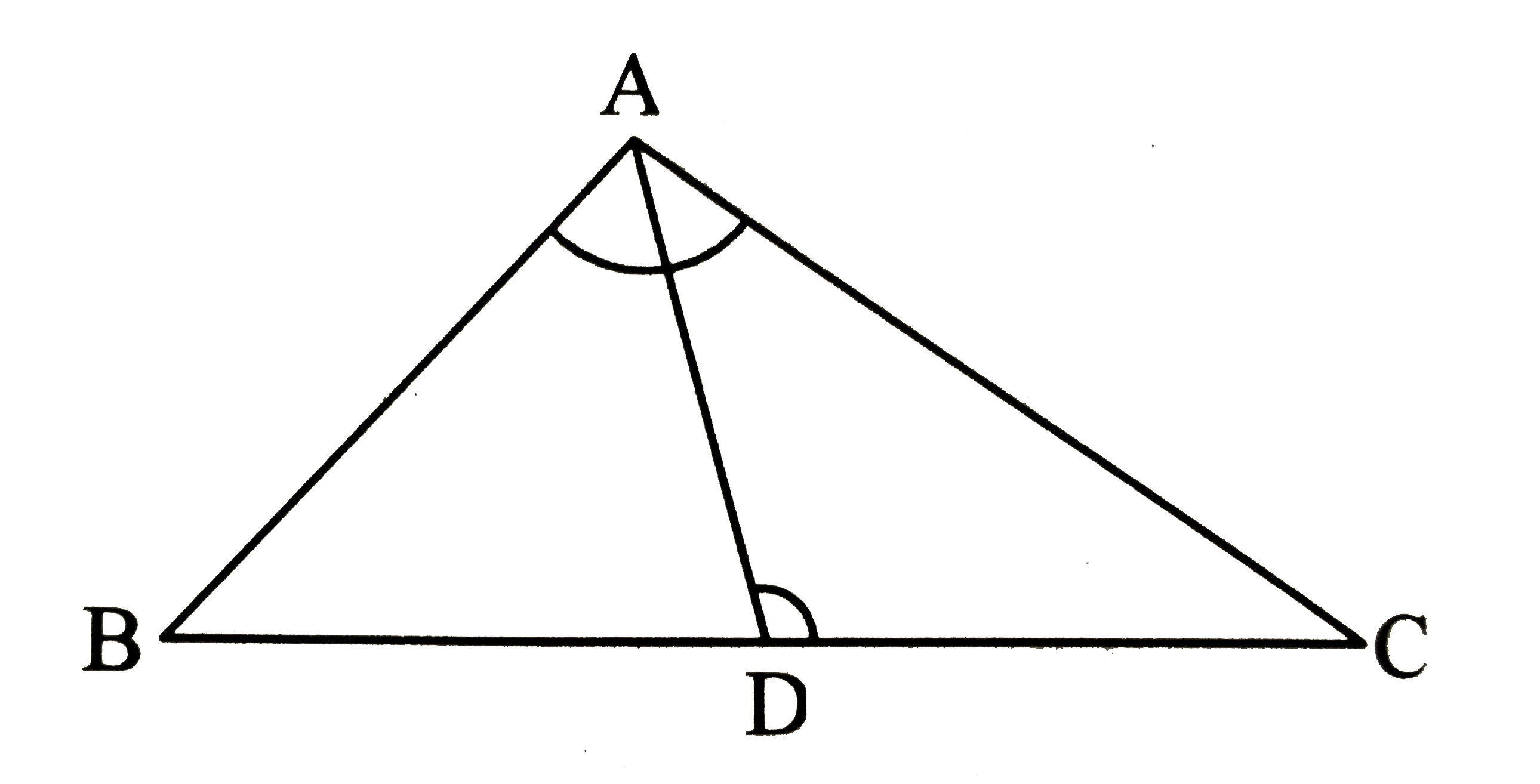 View Solution
View SolutionIf the diagonal BD of a quadrillateral ABCD bisects both ∠Band∠D. Prove that ABBC=ADCD.
View SolutionIn the figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C. Prove that AB = AD and CB = CD.
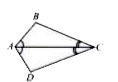 View Solution
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIn rectangle ABCD, E is the midpoint of side BC. Prove that, AE = DE.
View Solution