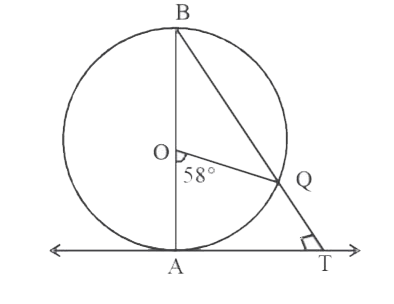
In the given figure, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘, find ∠ATQ.

∠AOQ=58∘
⇒∠ABQ=12∠AOQ=29∘ [∵ the angle subtended by an arc at the centre is double the angle subtened by it at any point on the remaining part of the circle]
⇒∠ABT=29∘.
Now, AT is a tangent at A and OA is the radius through the point of contact A.
∴OA⊥AT, i.e., ∠OAT=90∘⇒∠BAT=90∘.
In ΔBAT, we have
∠BAT+∠ABT+∠ATB=180∘
⇒90∘+29∘+∠ATB=180∘⇒∠ATB=61∘.
∴∠ATQ=∠ATB=61∘.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A16videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
 A30∘B60∘C45∘D25∘
A30∘B60∘C45∘D25∘ - Question 2 - Select One
In the given figure, O is the centre of a circle , AB is a chord and AT is the tangent at A. If ∠AOB=100∘ then ∠BAT is equal to
A40∘B50∘C90∘D100∘
In the given figure, AOB is a diameter of a circle with centre O. Find tan A tan B.
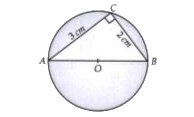 View Solution
View SolutionIn the giben figure, AB is the diameter of the circle, with centre O and AT is the tangent. Calculate the calue of x.
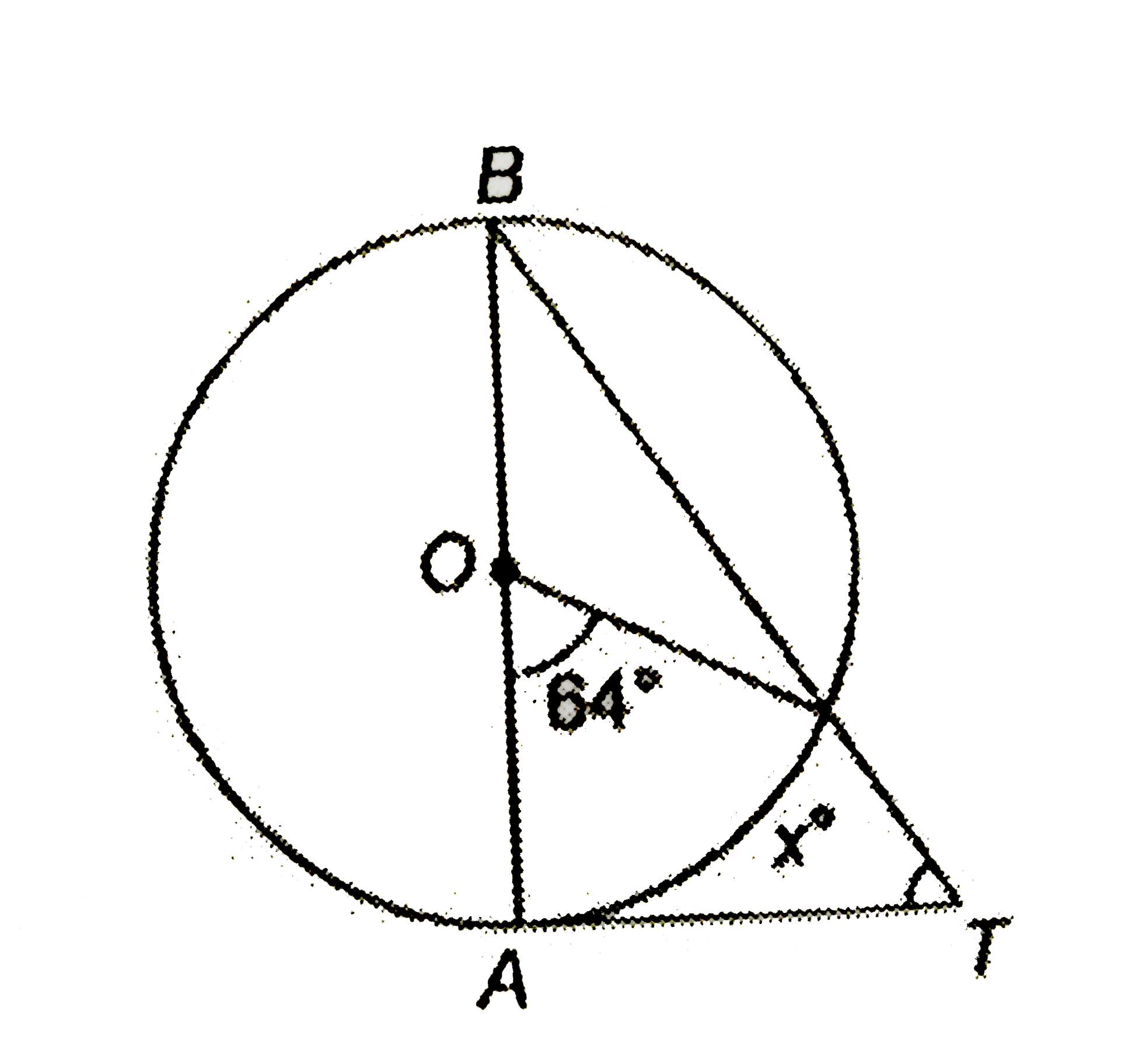 View Solution
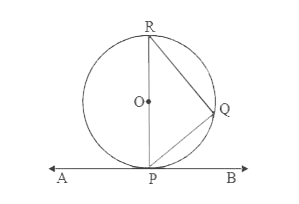
View SolutionIn the given figure, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT=60∘ find ∠PRQ
View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If ∠ACX=35∘, then what is the value (in degrees) of ∠CAB ?
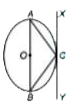 View Solution
View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If ∠ACX=35∘, then what is the value (in degrees) of ∠CAB?
 View Solution
View SolutionIn the given figure, AB is a tangent to a circle with centre O. Prove ∠BPQ=∠PRQ.
 View Solution
View Solution