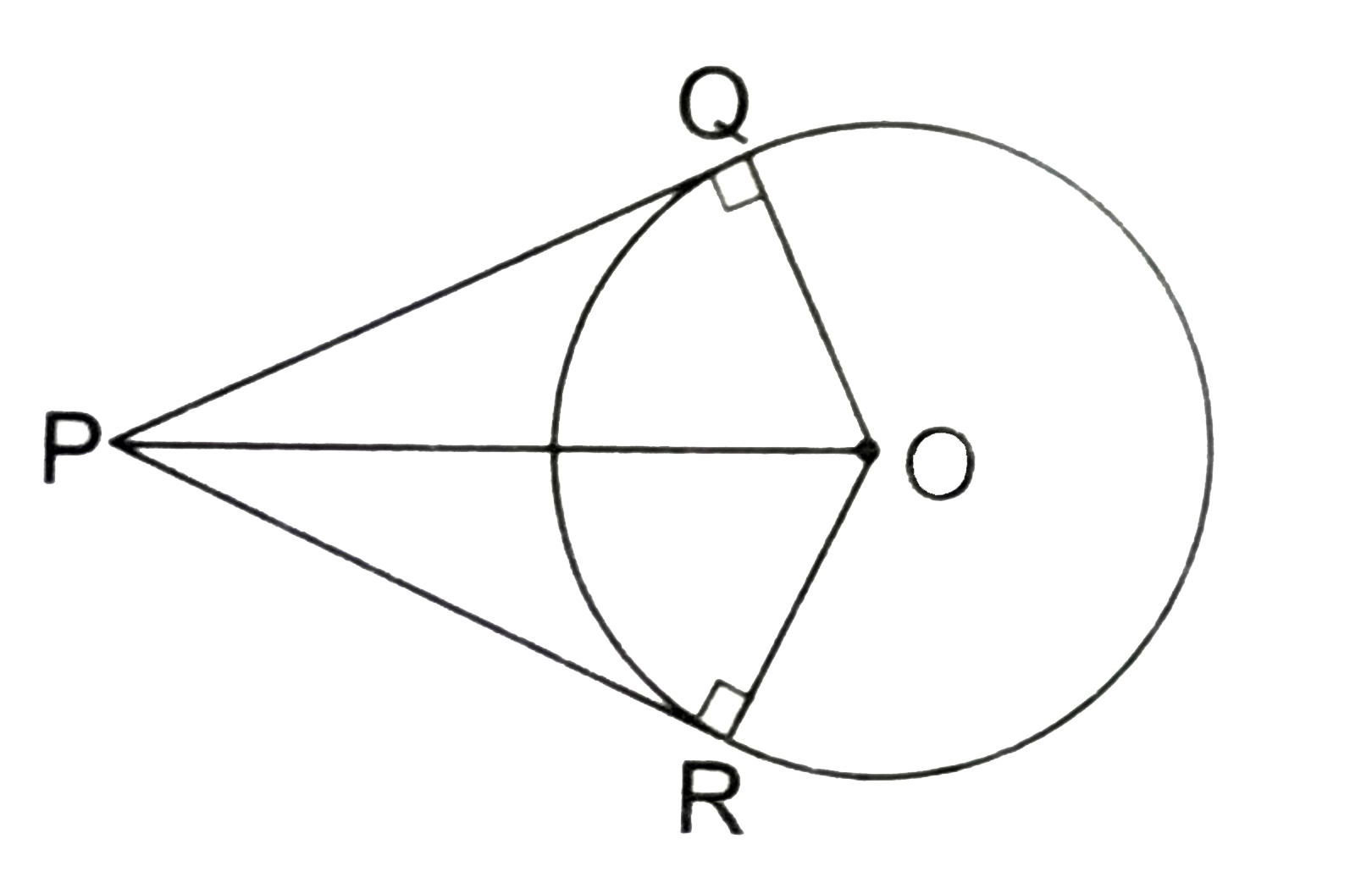
O is the centre of a circle of radius 5cm. At a distance of 13cm from O, a point P is taken. From this point, two tangents PQ and PR are drawn to the circle. Then, the area of quad. PQOR is
60cm2
32.5cm2
65cm2
30cm2
Clearly, OQ=OR=5cm, ∠OQP=∠ORP=90∘ and OP=13cm
∴PQ2=OP2−OQ2=(13)2−(5)2=169−25=144⇒PQ=√144=12cm.
∴ar(ΔOQP)=12×PQ×OQ=(12×12×5)cm2=30cm2.
Similarly, ar(ΔORP)=30cm2.
∴ar(quadPQOR)=(30+30)cm2=60cm2
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Assertion-and-Reason
1 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Test Yourself
20 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Multiple Choice Questions (Mcq)
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
Draw two tangents to a circle of radius 4 cm from a point T at a distance of 6 cm from its centre.
View SolutionFrom a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Find the area of quadrilateral PQOR,
View Solution
Knowledge Check
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is :
A60 cm2B65 cm2C30 cm2D32.5 cm2From a point P which is at a distance of 13 cm from the center O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle is drawn. Then, the area of the quadrilateral POQR is
A60cm2B65cm2C30cm2D32.5cm2From a point P which is at a distance of 13 cm from centre O of a circle of radius 5 cm, in the same plane, a pair of tangents PQ and PR are drawn.area of quadrilateral PQOR is
A65cm2B60cm2C30cm2D90cm2
Draw a circle of radius 2.5 cm. Take a point at a distance of 5 cm from the centre of the circle. From point P, draw two tangents to the circle.
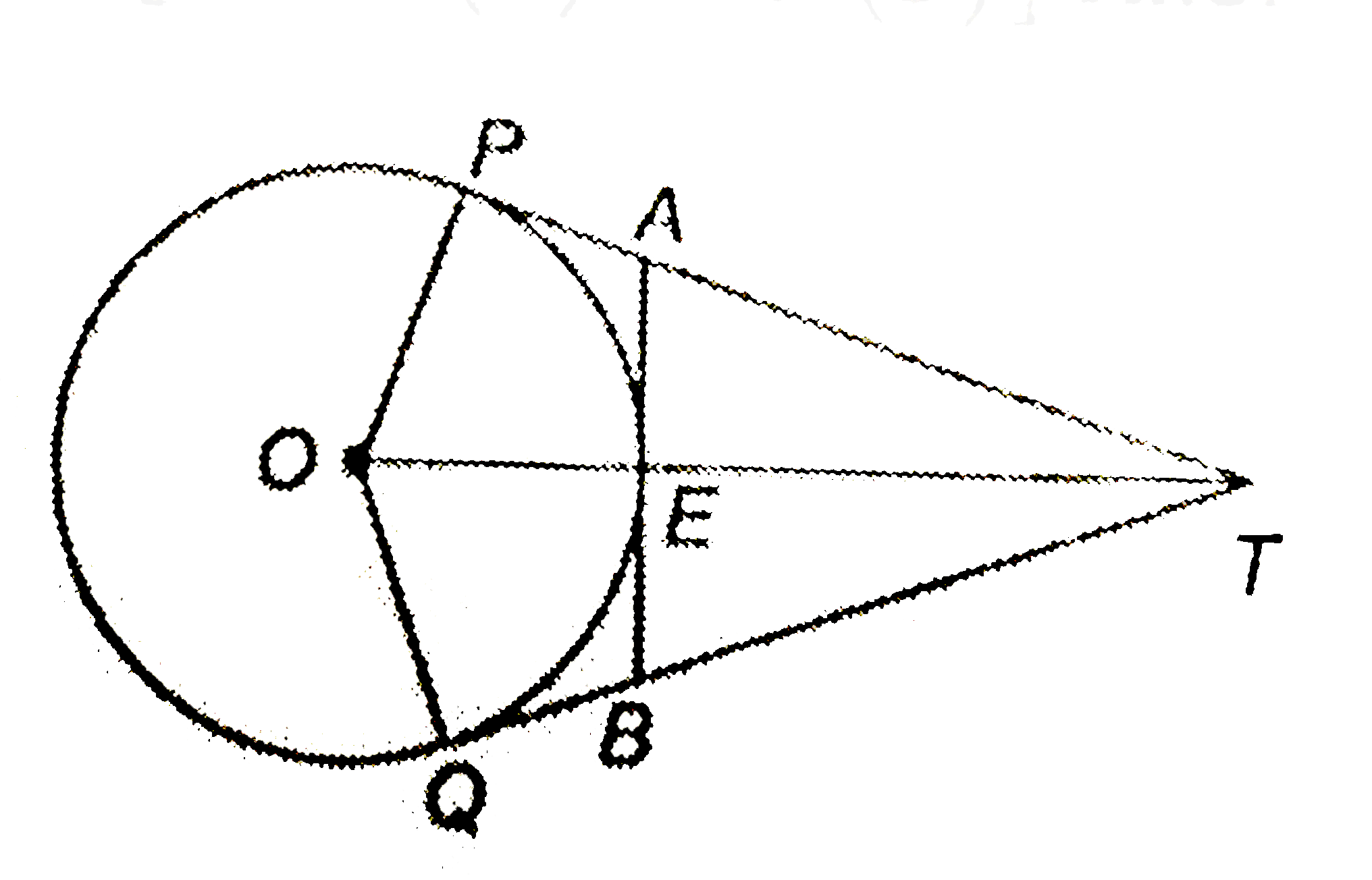
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
View SolutionDraw a circle of radius 3 cm. Take a point P at a distance of 5 cm from the centre of the circle. From P, construct a pair of tangents to the circle.
View SolutionFind the length of tangent drawn to a circle of radius 6 cm, from a point at a distance of 10 cm from the centre.
View SolutionFrom a point P which is at a distance of 10 cm from the centre O of a circle of radius 6 cm, a pair of tangents PQ and PR to the circle at point Q and P respectively, are drawn. Then the area of the quadrilateral PQOR is equal to
View Solution
