A small manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to another machine for finishing. The number of man-hours of labour required in each shop for the production of each unit of A and B and the number of man-hours for the firm available per week are as follows:

Formulate it in form of linear inequations .Draw the graph showing the solution of all these inequations .


Suppose that the firm manufactures x units of A and y units of B.
∴ number of man-hours for A and B in the foundry = 10x+6y,
and number of man-hours for A and B in the machine shop =5x+4y .
∴ 10x+6y≤1000and5x+4y≤600
Clearly x≥0andy≥0 [∵ number of units connot be nagative
SCALE 1 small division = 2 units

First we draw the graph of 10x+6y≤1000.
Consider the equation, 10x+6y=1000.
10x+6y=1000⇒5x+3y=500.
The values of (x, y) satisfying 5x + 3y = 500 are:

Plot the points A(70, 50) and B(40, 100) on a graph paper and join them by the thick line AB.
Consider (0, 0). It does not lie on 5x+3y=500.
Also, (0, 0) satisfies 10x+6y≤1000
Therefore, the line AB and the part of the plane separated by
AB, containing (0, 0), represent the graph of 10x+6y≤1000
(ii) Now ,we draw the graph of 5x+4y≤600
Consider the line, 5x + 4y = 600.
5x+4y=600⇒x120+y150=1
This line meets the axes at C(120, 0) and D(0, 150).
Plot these points on the same graph paper as above and join them by the thick line CD
Now, consider (0, 0). It does not lie on 5x + 4y = 600.
Also, (0, 0) satisfies the inequatiori 5x+4y≤600.
So, the line CD and that part of the plane separated by CD
containing (0, 0), represent the graph of 5x+4y≤600
x≥0 is represented by the y-axis and the part of the plane on its right side.
y≥0 is represented by the x-axis and the plane above the x-axis
Clearly, the shaded region together with its boundary represents the solution set of the given inequations.
Topper's Solved these Questions
- LINEAR INEQUATIONS (IN TWO VARIABLES )BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN TWO VARIABLES )EXERCISE - EXERCISE 7
22 Videos
- LINEAR INEQUATIONS (IN ONE VARIABLE)BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN ONE VARIABLE)EXERCISE - EXERCISE 6B
12 Videos
- LogarithmBOOK - RS AGGARWALCHAPTER - LogarithmEXERCISE - Exercise 1
9 Videos
Similar Questions
A small manufacturing firm produces two types of gadgets A and B which are first processed in the foundry, the sent to the machine ship for finishing. The number of man hours of labour required in each shop for the production of each unit of A and B and the number of man hours the firm has available per week are as follows: Gadget Foundry Machine – shop A 10 5 B 6 4 Firm’s capacity per week 1000 600 The profit the salt A is Rs. 30 per unit as compared with Rs. 20 per unit of B. the problem is to determine the weekly production of gadgets and B, so that the total profit is maximized. Formulate this problem as a LPP.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
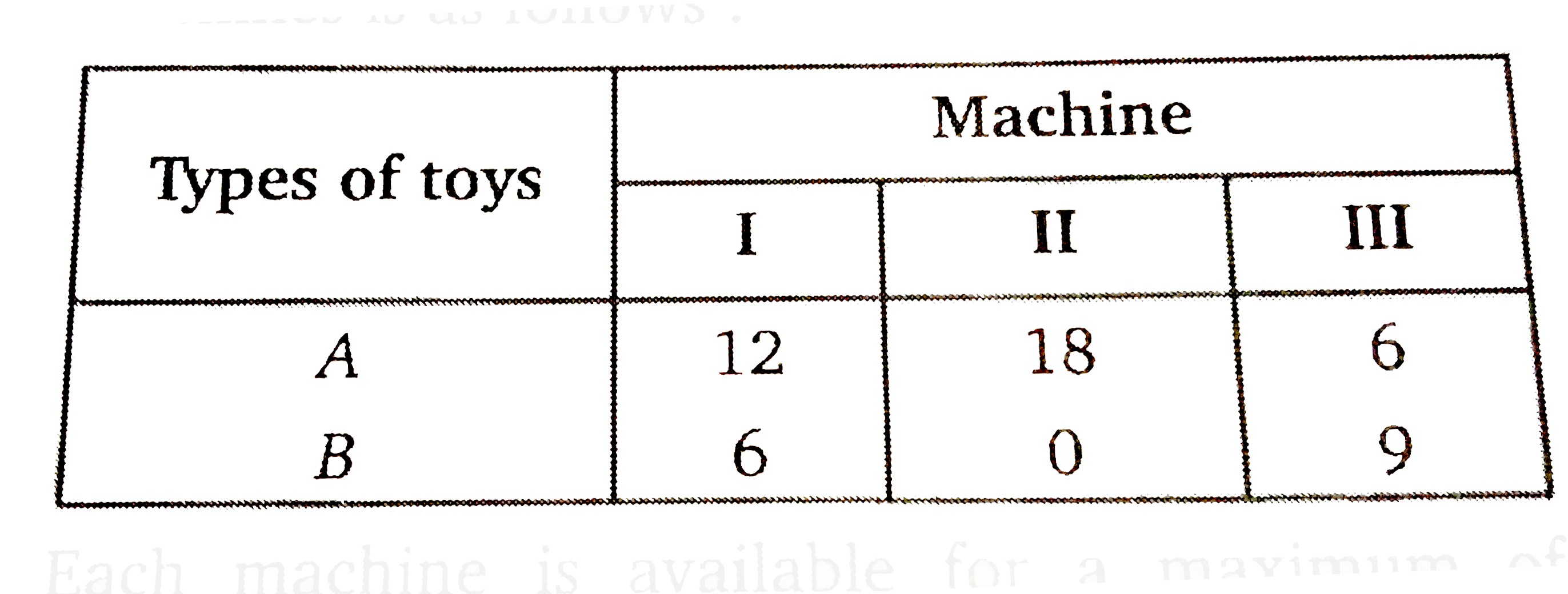 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View Solution
Knowledge Check
A firm makes pants and shirts . A shirt takes 2 hours on machine and 3 hours of man lobour while a pant takes 3 hours on machine and 2 hours of man labour .In a week , there are 70 hours of machine and 75 hous of man lobour available . If the firm dertermines to make x shirts and y pants per week , then for this linear constraints are
Ax≥0,y≥0,2x+3y≥70,3x+2y≥75Bx≥0,y≥0,2x+3y≤70,3x+2y≥75Cx≥0,y≥0,2x+3y≥70,3x+2y≤75Dx≥0,y≥0,2x+3y≤70,3x+2y≤75
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs. 7 profit and that of B at a profit of Rs. 4. Find the production level per day for maximum profit graphically.
View SolutionA manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs. 7 profit and that of B at a profit of Rs. 4. Find the production level per day for maximum profit graphically.
View SolutionA manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View SolutionA manufacturing companu makes two types of teaching aids A and B of Mathematics for Class X. Each type of A requires 9 labour hours for fabircating and 1 labour for finishing. Each type of B requires 12 labour hours for fabircating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of 80 on each piece of type A and 120 on each piece of type B. How many pieces of type A and types B should be manufactured per week to get a maximum profit? Formulae this as Linear Programming Problems and solved it. Identify the feasible region from the rough sketch.
View SolutionA manufacturing company makes two types of teaching aids A and B . Each type of A requires 9 labour hours for fabricating and 1 labour hours for finishing.Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing.For fabricating and finishing, the maximum labour hours abailable per week are 180 and 30 respectively.The company makes a profit of ₹ 80 on each type A and ₹ 120 on each type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically.What is the maximum profit per week?
View SolutionA manfufacturer produces two products A and B.Both the products are processed on two different machines.The available capacity of the first machines is 12 hours and that of second machine is 9 hours.Each unit of product A require 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on the second machine.Each unit of product A is sold at a profit of ₹ 5 and B at a profit ₹ 6. Find the productive level for maximum profit graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades.Both the products require machine time as well as craftsman time in the making.The number of hours required for producing 1 unit of each and the corresponding profit is given in the following table:
In a day,the factory has availability of not more than 42 hours of machine time and 24 hours of craftsman time.
Assuming that all items manufactured are sold,how should the manufacturer schedule his daily production in order to maximise the profit?Formulate it as an LPP and solve it graphically
View Solution
