यदि OABC एक चतुष्फलक इस प्रकार है कि OA2+BC2=OB2+CA2=OC2+AB2, तब
OA⊥BC
OB⊥CA
OC⊥AB
AB⊥BC
The correct Answer is:A, B, C, D
Step by step video, text & image solution for यदि OABC एक चतुष्फलक इस प्रकार है कि OA^(2)+BC^(2)=OB^(2)+CA^(2)=OC^(2)+AB^(2), तब by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिविमीय ज्यामिति BOOK - ARIHANT HINDICHAPTER - त्रिविमीय ज्यामिति EXERCISE - प्रश्नावली (स्तर 2)(श्रृंखलाबद्ध- बोधन प्रकार )
3 Videos
- त्रिविमीय ज्यामिति BOOK - ARIHANT HINDICHAPTER - त्रिविमीय ज्यामिति EXERCISE - प्रश्नावली (स्तर 2)(दृढकथन-कारण प्रकार)
7 Videos
- त्रिविमीय ज्यामिति BOOK - ARIHANT HINDICHAPTER - त्रिविमीय ज्यामिति EXERCISE - प्रश्नावली (स्तर 2)(केवल एक विकल्प सही है)
40 Videos
- त्रिभुजों के गुण,ऊंचाई एवं दुरी BOOK - ARIHANT HINDICHAPTER - त्रिभुजों के गुण,ऊंचाई एवं दुरी EXERCISE - प्रश्नावली (स्तर 2) (विगत वर्षों के प्रश्न)
3 Videos
- त्रिविमीय ज्यामिति का परिचयBOOK - ARIHANT HINDICHAPTER - त्रिविमीय ज्यामिति का परिचयEXERCISE - प्रश्नावली
32 Videos
Similar Questions
दो रेखाएँ x−32=y−23=z−1λतथा x−23=y−32=z−23एक समतलीय हैं।
sin−1(sinλ)का मान है
View Solutionवक्तव्य I यदि r=xˆi+yˆj+zˆk हो, तो समीकरण r×(2ˆi−ˆj+3ˆk)=3ˆi+ˆk एक सरल रेखा निरूपित करता है।
वक्तव्य II यदि r=xˆi+yˆj+zˆk हो, तो समीकरण r×(ˆi+2ˆj−3ˆk)=2ˆi−ˆj एक सरल रेखा निरूपित करता है
View Solutionशीर्ष (1,0,1),(2,−1,3) तथा (−1,2,−1) वाले त्रिभुज का क्षेत्रफल है
View Solutionएक सम बहुभुज के लिए माना अन : वृत तथा परिवृत की त्रिज्याऍं क्रमश r तथा R निम्नलिखित में से कौन –सा प्रकथन मिथ्या है।
View SolutionXy- समतल से समांत समतल लंब होगा
View SolutionIf OABC is a tetrahedron such thatOA2+BC2=OB2+CA2=OC2+AB2 then
View SolutionLet O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
View SolutionThe OABC is a tetrahedron such that OA2+BC2=OB2+CA2=OC2+AB2,then
View Solutionत्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि
AB+BC+CA<2(OA+OB+OC)
View Solutionत्रिभुज ABC के अन्तः भाग में O कोई बिन्दु है | सिध्द करो कि
OA+OB+OC>12(AB+BC+CA)
View SolutionIf OABC be a regular tetrahedron such that OA2+BC2=OB2+CA2=OC2+AB2 then
View SolutionIf O is point in the exterior of △ABC,show that 2(OA+OB+OC)>(AB+BC+CA)
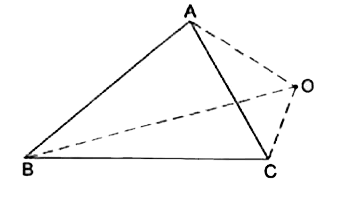
View SolutionO is any point in the exterior of a ΔABC. Prove that 2(OA+OB+OC)>(AB+BC+CA)
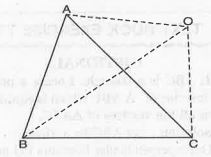 .
.
View SolutionIf OABC is a tetrahedron such that OA2+BC2=OB2+CA2=OC2+AB2= then
View SolutionIf 0 is a point in the exterior of an ABC, then show that OA+OB +OC gt (1)/2 (AB + BC + CA)
View Solution
