Square : Diamond :: Circle : ?
Smooth
Round
Oval
Ball
The correct Answer is:C
Second is the shape obtained by pulling the opposite ends of the first.
Topper's Solved these Questions
- ASSIGNMENT-3(ANALOGY)BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-3(ANALOGY)EXERCISE - TYPE 2 [Choosing the Analogous Pair]
20 Videos
- ASSIGNMENT-3(ANALOGY)BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-3(ANALOGY)EXERCISE - TYPE 3 [Number Analogy]
30 Videos
- ASSIGNMENT-10 (CLASSIFICATION)BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-10 (CLASSIFICATION)EXERCISE - TYPE-4
20 Videos
- ASSIGNMENT-7 (PUZZLE TEST)BOOK - MCGROW HILL PUBLICATIONCHAPTER - ASSIGNMENT-7 (PUZZLE TEST)EXERCISE - MCQs
20 Videos
Similar Questions
A square and a circle are placed such that the centre of the circlelies in the centre of the square. The region inside the square butoutside the circle has the same area as the region inside the circlebut outside the square. What is the quotient between the diameterof the circle and the side of the square?
View SolutionA square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles is
View Solution
Knowledge Check
A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
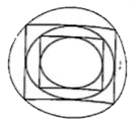
What is the ratio of sum of circumference of all the circles to the sum of perimeters of all the squares ?A(2+√3)πRB(3+√2)πRC3√3πRDnone of theseA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
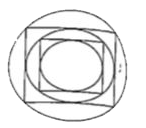
What is the sum of areas of all the squares shown in the figure ?A3R2B3√2R2C3√2R2Dnone of theseA square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles isA4πR2(1−(12)n)B2πR2(1−(12)n)C3πR2(1−(13)n)DπR2(1−(12)n)
A square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .

What is the radius of the inner - most circle ?
View SolutionA square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
View SolutionA square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
View SolutionA square and a circle have equal perimeters. The ratio of the area of the square to the area of the circle is
View SolutionThe areas of a square and a circle are equal. The radius of the circle is r and the side of the square is S.Find the circumference of the circle in terms of S.
View Solution
