A tower BCD surmounted by a spire DE stands on a horizontal plane. At the extremity A of a horizontal line BA it is found that BC and DE subtend equal angles. If BC = 3 m, CD = 28 m and DE = 5 m, then BA is equal to
A
√18×93
B
√36×93
C
√34×93
D
√34×36
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - SOLVED EXAMPLES (LEVEL 2 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))
15 Videos
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - SOLVED EXAMPLES (NUMERICAL ANSWER TYPE QUESTIONS )
5 Videos
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
3 Videos
- ELLIPSEBOOK - MCGROW HILL PUBLICATIONCHAPTER - ELLIPSEEXERCISE - Previous Years B-Architecture Entrance Examination Papers
6 Videos
- HYPERBOLABOOK - MCGROW HILL PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - QUESTION FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
8 Videos
Similar Questions
Knowledge Check
In the figure, if DE || BC, AD = 3 cm, BD = 4 cm, and BC = 14 cm, then DE equals :
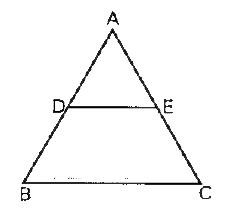 A7 cmB6 cmC4 cmD3 cm
A7 cmB6 cmC4 cmD3 cmIn ΔABC,DE∣∣BCsuch that ADBD=35. If AC=5.6cm, then AE is equal to
A4.2 cm.B3.1 cm.C2.8 cm.D2.1 cm.In ΔABC,∠C=90∘. D is the midpoint BC : and DE⊥AB at E. If AB =13 cm and BE =5 cm, then the area of the square drawn on BC is equal to :
AA)130cm2BB)100cm2CC)120cm2DD)125cm2
In figure-2, DE∣∣BC. If ADDB=32 and AE=2.7 cm then EC is equal to
View SolutionIn figure-2, DE∣∣BC. If ADDB=32 and AE=2.7 cm then EC is equal to
View SolutionOne-fifth of the area of a triangle ABC is cut off by a line DE drawn parallel to BC such that D is on AB and E is on AC. If BC = 10 cm, then what is DE equal to ?
View SolutionFind the area of the quadrilateral ABCD in which AB = 9 m, BC = 40 m, ∠ABC=90∘, CD = 15 m and AD = 28 m.
View SolutionIn the figure, ∠ADC=90∘,
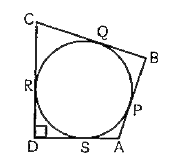
BC=38 cm,CD=28 cmandBP=25 m. Find the radius of the circle.
View Solution