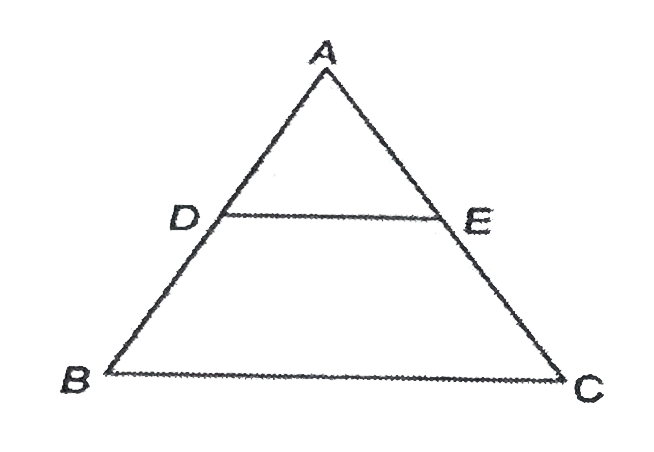
In figure-2, DE∣∣BC. If ADDB=32 and AE=2.7 cm then EC is equal to
2.0 cm
1.8 cm
4.0 cm
2.7 cm
The correct Answer is:B
To solve the problem, we will use the Basic Proportionality Theorem (also known as Thales' theorem), which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
1. Identify Given Information:
- We are given that DE∥BC.
- The ratio ADDB=32.
- The length AE=2.7 cm.
- We need to find EC.
2. Apply the Basic Proportionality Theorem:
- According to the theorem, since DE∥BC, we can write:
ADDB=AEEC
- Substituting the known values:
32=2.7EC
3. Cross-Multiply to Solve for EC:
- Cross-multiplying gives:
3⋅EC=2⋅2.7
- Simplifying the right side:
3⋅EC=5.4
4. Isolate EC:
- Divide both sides by 3:
EC=5.43
- Calculating the division:
EC=1.8 cm
5. Conclusion:
- Therefore, the length of EC is 1.8 cm.
Final Answer:
EC=1.8 cm.
- We are given that DE∥BC.
- The ratio ADDB=32.
- The length AE=2.7 cm.
- We need to find EC.
- According to the theorem, since DE∥BC, we can write:
ADDB=AEEC
- Substituting the known values:
32=2.7EC
- Cross-multiplying gives:
3⋅EC=2⋅2.7
- Simplifying the right side:
3⋅EC=5.4
- Divide both sides by 3:
EC=5.43
- Calculating the division:
EC=1.8 cm
- Therefore, the length of EC is 1.8 cm.
EC=1.8 cm.
Similar Questions
In the given figure, DE||BC and ADDB=23if AE=3.7 cm , find EC.

View SolutionIn the figure DE is parallel to BC and ADDB=23 if AE = 3.7 cm find EC.
View SolutionIn the figure, EF || AC, BC = 10 cm, AB = 13 cm and EC = 2 cm, find AF
View Solutionin a figure DE||BC AD=3cm, BD =4cm and BC=14cm, then DE equals
View SolutionIn ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB.
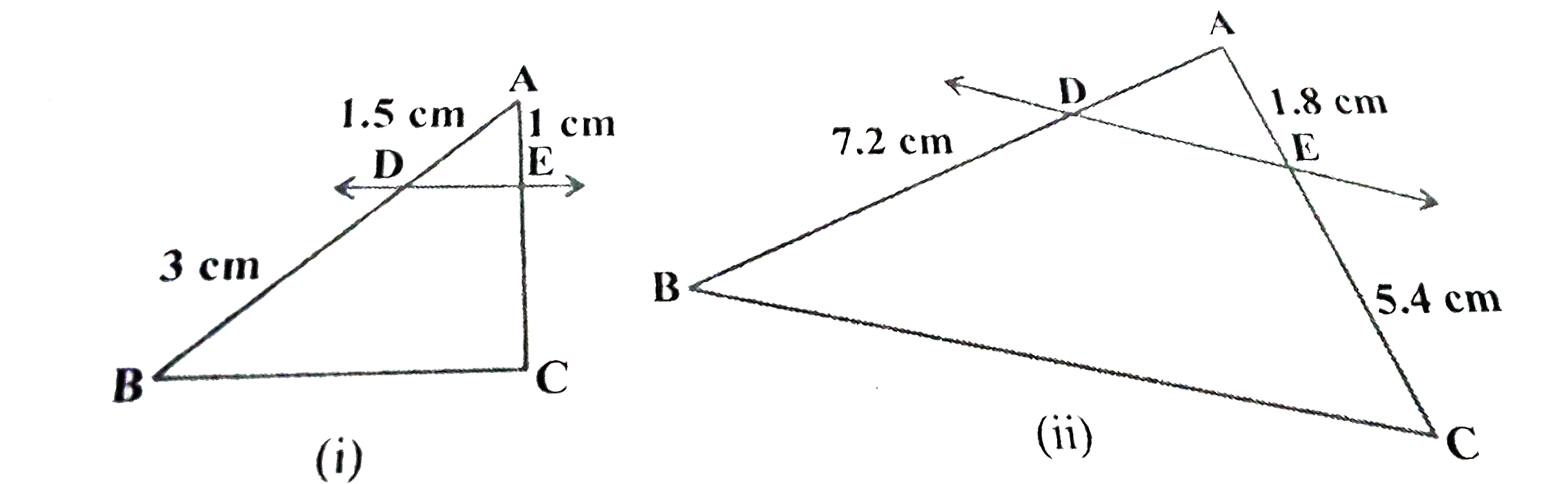
View SolutionIn Figure (i) and (ii), DE||BC. Find EC in (i) and AD in (ii).
View SolutionIn the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
View SolutionIn the given figure, ΔABC~ΔADE. If AE:EC=4:7andDE=6.6cm, find BC. If *x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of ‘x'.

View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

Prove that ΔDEF is similar to ΔCBF.Hence, find EFFB.
View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

What is the ratio of the areas of ΔDEF and ΔBFC ?
View Solution
