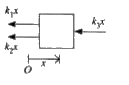
At equilibrium, the springs are released, mass M is oscillating under the influence of three springs, $k_{1}, k_{2} and k_{3}$ as shown. Its frequency $(υ)$ of oscillation is $\frac{1}{2 π} \sqrt{\frac{k_{e q}}{M}}$ , where $k_{e q}$ I such that

A

$k_{e q} = k_{1} + k_{2} + k_{3}$

B

$k_{e q} = \frac{k_{1} + k_{2} + k_{3}}{3}$

C

$\frac{1}{k_{e q}} = \frac{1}{k_{1}} + \frac{1}{k_{2}} + \frac{1}{k_{3}}$

D

$k_{e q} = (k_{1} + k_{2} - k_{3})$

Text Solution

Verified by Experts

The correct Answer is:A

When the mass M is displaced slightly to the right, the resultant forces acting on the mass M is as shown.
$F_{net} = - (k_{1} + k_{2} + k_{3}) . x,$
Thus, $k_{e q} = k_{1} + k_{2} + k_{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two springs are joined and connected to mass m as shown. If the springs separately have force constants $K_{1}$ and $K_{2}$ , then frequency of oscillation of mass m is

A $\frac{1}{2 π} \sqrt{\frac{K_{1} K_{2}}{(K_{1} + K_{2}) m}}$
B $2 π \frac{\sqrt{(K_{1} + K_{2}) m}}{K_{1} K_{2}}$
C $2 π \sqrt{\frac{K_{1} K_{2}}{m}}$
D $\frac{1}{2 π} \sqrt{\frac{m}{K_{1} + K_{2}}}$
Question 2 - Select One
Two spring are connected toa block of mass $M$ placed a frictionless surface as shown if both the spring have a spring constant $k$ the frequency of oscillation block is

A $\frac{1}{2 π} \sqrt{\frac{k}{2 M}}$
B $\frac{1}{2 π} \sqrt{\frac{k}{M}}$
C $\frac{1}{2 π} \sqrt{\frac{2 k}{M}}$
D $\frac{1}{2 π} \sqrt{\frac{M}{k}}$
Question 3 - Select One
An object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
A $A \sqrt{k / m}$
B $A^{2} k / m$
C $A \sqrt{m / k}$
D $A m / k$

MTG GUIDE-OSCILLATIONS AND WAVES -AIPMT / NEET MCQs

Home
Ask Doubt
Profile