Consider a long solenoid of radius R which has n turns per unit length. A time dependent current I=I0sinωt flows solenoid, magnitude of electric field at a perpendicular distance r<R, from the axis of symmetry of solenoid is found to be E=α4ωμ0nI0rcosωt, where α is pure number and μ0 is permability of free space. Find α
μ0πb2n1n2L
μ0πa2n1n2L2
μ0πa2n1n2L
μ0πb2n1n2L2
The correct Answer is:C
The mutual inductance of the system is
M=μ0n1n2πa2L
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (INSTANTANEOUS, AVERAGE AND RMS VALUE OF ALTERNATING CURRENT/ VOLTAGE)5videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (AC CIRCUITS CONTAINING RESISTOR, INDUCTOR OR CAPACITOR)3videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTSEXERCISE - NEET CAFE TOPICWISE PRATICE QUESTIONS (LENZ.S LAW)1videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS
- BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs30videos
DUAL NATURE OF MATTER AND RADIATION
- BOOK - MTG GUIDECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - AIPMT/NEET(MCQs)15videos
ELECTROMAGNETIC WAVES
Similar Questions
A long straight solenoid has n turns per unit length. An alternating current I=Imsinωt flows throught it. Find the displacement current density as a function of the distnace r from the solenoid equals R.
View SolutionThe current in a long solenoid of radius R and having n turns per unit length is given by i=i0sinωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid and the coil.
View Solution
Knowledge Check
- Question 1 - Select One
A solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
Aμ0nI0ωR22rsinωtBμ0nI0ωR2rsinωtCμ0nI0R22rsinωtDzero - Question 2 - Select One
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
AaniBniCniaDn2i - Question 3 - Select One
A conducting ring of radius b is placed coaxially in a long solenoid of radius a (b < a) having n turns per unit length. A current i=i0, cosωt flows through the solenoid. The induced emf in the ring is
AZeroBμ0ni0πa2ωCμ0ni0πa2cosωtDμ0ni0πb2ωcosωt
A long solenoid with closely wound turns has n turns per unit of its length. A steady current I flows through this solenoid. Use Ampere's circuital law to obtain an expression, for the magnetic field, at a point on its axis and close to its mid point.
View SolutionA tightly wound solenoid of radius 'a' and length 'l' has n turns per unit length. It carries an electric current i. Magnetic field at a distance l4 from one of the end (inside the solenoid on its axis) is B=μ0ni(√5+3)√K for l=4a. Then find the value of K.
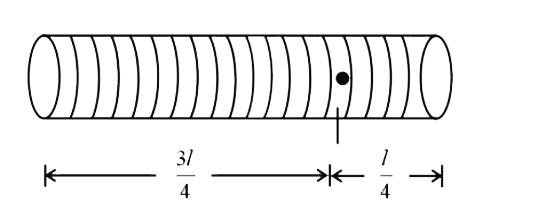 View Solution
View SolutionA long solenoid has n turns per unit length and carries a current i=i0sinωt. A coil of N turns and area A is mounted inside the solenoid and is free to rotate about its diameter that is perpendicular to the axis of the solenoid. The coil rotates with angular speed ω and at time t = 0 the axis of the coil coincides with the axis of the solenoid as shown in figure. Write emf induced in the coil as function of time.
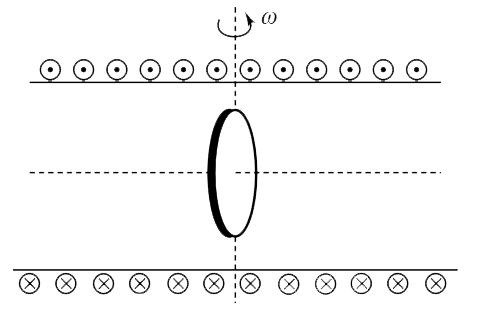 View Solution
View SolutionA solenoid of radius R and length L has a current I=I0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is
View SolutionThere is a long solenoid of radius 'R' having 'n' turns per unit length with current i flowing in it. A particle having charge 'q' and mass 'm' is projected with speed 'v' in the perpendicular direction of axis from a Point on its axis. Find maximum value of 'v' so that it will not collide with the solenoid.
View Solution

