Two conducting circular loops of radii $R_{1} and R_{2}$ are placed in the same plane with their centres coincidingt. Find the mutual inductane between them assuming $R_{2} < < R_{1}$ .

A

$\frac{R_{1}}{R_{2}}$

B

$\frac{R_{2}}{R_{1}}$

C

$\frac{R_{1}^{2}}{R_{2}}$

D

$\frac{R_{2}^{2}}{R_{1}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let a current $I_{1}$ flows through the outer circular coil of radius $R_{1}$ .
The magnetic field at the centre of the coil is B = $\frac{μ_{0} I_{1}}{2 R_{1}}$
As the inner coil of radius $R_{2}$ placed co-axially has small radius $(R_{2} < R_{1})$ , therefore $B_{1}$ may be taken constant over its crosssectional area. Hence, flux associated with the inner coil is
$ϕ_{2} = B_{1} π R_{2}^{2} = \frac{μ_{0} I_{1}}{2 R_{1}} π R_{2}^{2}$
As $M = \frac{ϕ_{2}}{I_{1}} = \frac{μ_{0} π R_{2}^{2}}{2 R_{1}} ∴ M \propto \frac{R_{2}^{2}}{R_{1}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two concentric co - planar circular loops of radius R and $r (< < R)$ are placed as shown in the figure. The mutual inductance of the system will be

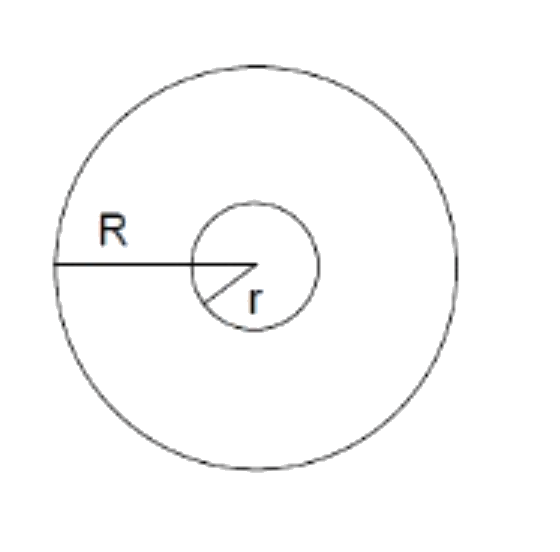A $\frac{π μ_{0} r^{2}}{2 R}$
B $\frac{π μ_{0} r^{2}}{4 R}$
C $\frac{π μ_{0} R^{2}}{4 r}$
D $\frac{π μ_{0} R^{2}}{2 r}$
Question 2 - Select One
Two conducting spheres of radii $r_{1}$ and $r_{2}$ are equally charged. The ratio of their potentral is-
A $r_{1}^{2} / r_{2}^{2}$
B $r_{2}^{2} / r_{1}^{2}$
C $r_{1} / r_{2}$
D $r_{2} / r_{1}$
Question 3 - Select One
Two concentric circular coils, one of small radius $r_{1}$ and the other of large radius $r_{2}$ such that $r_{1} < < r_{2}$ are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
A $\frac{μ_{0} π t r_{1}^{2}}{2 r_{2}}$
B $\frac{μ_{0} π t r_{2}^{2}}{2 r_{1}}$
C $\frac{μ_{0} π t r_{2}^{2}}{r_{1}}$
D $\frac{μ_{0} π t r_{1}^{2}}{r_{2}}$

MTG GUIDE-ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS-NEET CAFE TOPICWISE PRATICE QUESTIONS (SELF AND MUTUAL INDUCTANCE)

Home
Ask Doubt
Profile