A ray of light is incident on a glass slab of thickness t, at an angle i,r is the angle of refraction in the glass slab. Distance travelled in the glass slab is
tcosr
anr
tcosr
tsinr
The correct Answer is:C
To solve the problem of finding the distance traveled by a ray of light in a glass slab of thickness t, we can use some basic trigonometry. Let's break it down step by step.
Step 1: Understand the Geometry
When a ray of light enters a glass slab at an angle of incidence i, it refracts and travels through the slab at an angle of refraction r. The thickness of the slab is given as t.
Step 2: Identify the Points
Let's label the points:
- Point A: The point where the light enters the glass slab.
- Point B: The point where the light exits the glass slab.
- Point O: The point where the light is refracted inside the slab.
Step 3: Draw a Right Triangle
Inside the glass slab, we can visualize a right triangle formed by:
- The thickness of the slab t as one side (the vertical side).
- The distance traveled by the light in the glass slab as the hypotenuse.
Step 4: Use Trigonometry
In the right triangle OAB:
- The angle at point O is r.
- The side opposite to angle r is the thickness t.
- The hypotenuse is the distance traveled by the light in the slab, which we will denote as OA.
Using the cosine function:
cos(r)=AdjacentHypotenuse=BOOA
Here, BO is the thickness t.
Step 5: Rearranging the Equation
From the above equation, we can rearrange it to find OA:
OA=tcos(r)
Step 6: Conclusion
Thus, the distance traveled by the light in the glass slab is given by:
OA=tcos(r)
Final Answer
The distance traveled by the light in the glass slab is tcos(r).
---
When a ray of light enters a glass slab at an angle of incidence i, it refracts and travels through the slab at an angle of refraction r. The thickness of the slab is given as t.
Let's label the points:
- Point A: The point where the light enters the glass slab.
- Point B: The point where the light exits the glass slab.
- Point O: The point where the light is refracted inside the slab.
Inside the glass slab, we can visualize a right triangle formed by:
- The thickness of the slab t as one side (the vertical side).
- The distance traveled by the light in the glass slab as the hypotenuse.
In the right triangle OAB:
- The angle at point O is r.
- The side opposite to angle r is the thickness t.
- The hypotenuse is the distance traveled by the light in the slab, which we will denote as OA.
cos(r)=AdjacentHypotenuse=BOOA
Here, BO is the thickness t.
From the above equation, we can rearrange it to find OA:
OA=tcos(r)
Thus, the distance traveled by the light in the glass slab is given by:
OA=tcos(r)
The distance traveled by the light in the glass slab is tcos(r).
Topper's Solved these Questions
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - Check your NEET vitals
25 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
A light ray is incident on a plane glass slab of thickness ‘t’ at an angle of incidence ‘i’ as shown in the figure. If μ is the refractive index of glass. Then find time taken by the light ray to travel through the slab.
View SolutionA ray of light is incident on a galss slab making on angle of 30∘ with the surface . If the angle of refraction in glass is 33∘, the angle of deviation of the ray during its passage through the galss slab is
View Solution
Knowledge Check
A ray of light is incident on a glass slab making an angle of 30∘ with the surface. The angle of refraction in glass, if the refractive index of flass is 1.6 , is
A28∘B33∘C12∘D15∘A ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
A40∘B30∘42'C50∘D60∘A ray of light is incident on a glass slab at an angle of 45∘. If refractive index of glass be 1.6, what is the angle of refraction ?
A45.2∘B30∘C26.2∘D15.2∘
A ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
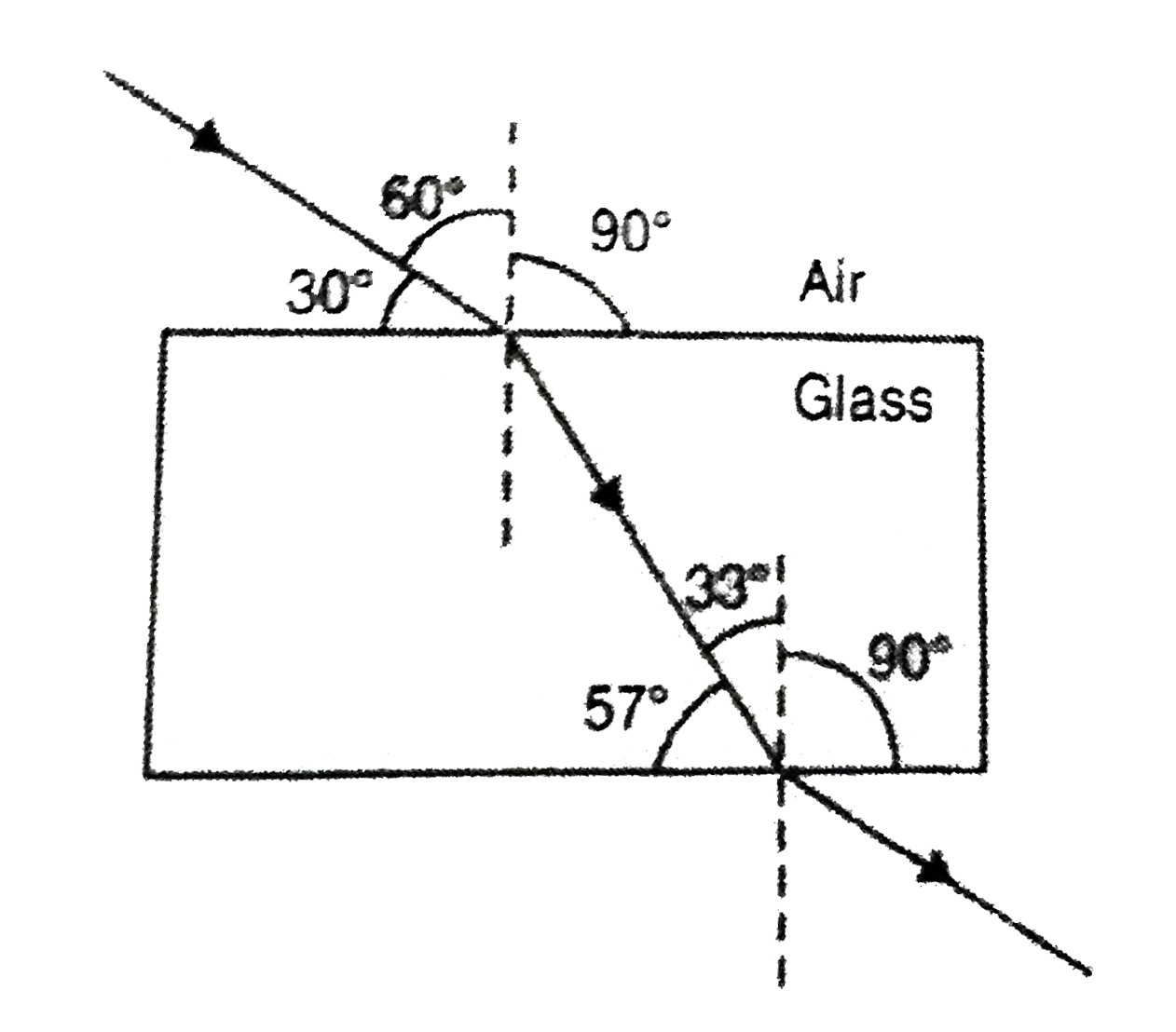
View SolutionA parallel beam of width 'a' is incident on the surface of glass slab (μ=3/2) at an angle 'I' and the angle of refraction in glass is 'r'. The width of the refracted parallel beam will be
View SolutionA beam of light is incident on glass slab making an angle of 60∘ with the surface. The angle of refraction and the velocity of light in glass of R.I. 1.5 are
View SolutionOrdinary light incident on a glass slab at the polarising angle suffers a deviation of 34∘ . The velue of the angle of refraction in glass in this case is
View SolutionA ray of light incident normally on a glass slab of refractive index 3/2, travels a distance of 6 cm in glass in time t. What will be the distance travelled by the ray in the same time (t) if it travels in air ?
View Solution
