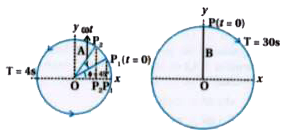
Figures depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.
 Solution in Gujrati
Solution in Gujrati
(a) As shown in figure, suppose a particle moving with uniform circular motion is at P1 at time t=0 and makes and angle ϕ=45∘(π4rad) with positive x-axis. After time t1 it covers an angle ωt and reaches at P2 and makes an angle θ=ωt+ϕ with positive x-axis.

Makes an angle θ=2πTt+π4
The projection of OP on the x-axis at time t is given by x(t)=Acos(2πTt+π4) have OP2=Acos(ωt+ϕ)
It t=4s then, x(t)=Acos(2π4t+π4)=Acos(π4+π4)=Asin(π)4.
Which is a SHM of amplitude A, period 4s and an initial phase =π4rad.
(b) As shown in figure, suppose a particle moving with uniform circular motion is on P at time t=0 and makes an angle ϕ=90∘=(π2) with positive x-axis after a time t, it covers an angle of ωt and reaches at P1 with clockwise direction and makes an angle of θ=π2−ωt. The projection of P.1 on the x-axis OP.1.

x(t)=Bcosθ=Bcos(π2−ωt)=Bsinωt
=Bcos(ωt−π2) [∴cos(−θ)=cosθ]
∴x(t)=Bcos(π15t−π2)
This represents a SHM of amplitude B, period T= 30s and an initial phase of −π2.
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)
48 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)
9 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-A (TRY YOURSELF)
64 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
Which of the following examples represent periodic motion?
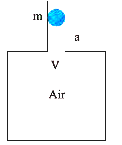
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionWhat is motion ?
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View Solutiondepict two circulat mothions. The radius of the circle, the period of revolution, the initial position and sense of revolution are indicated in the figures. Obtain the simple harmonic motinosof the x-projection of the radius vector of the rotating particle P in each case.
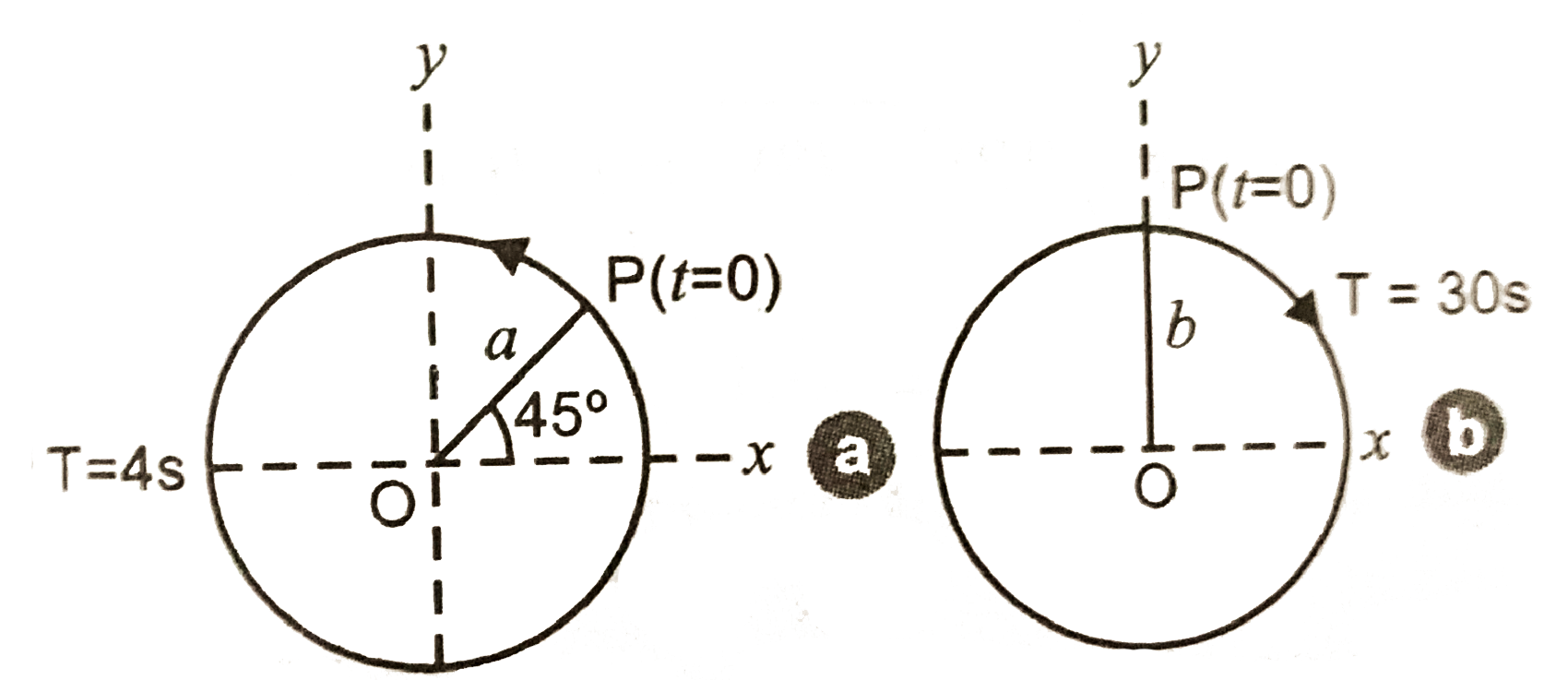
View Solutionthe circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
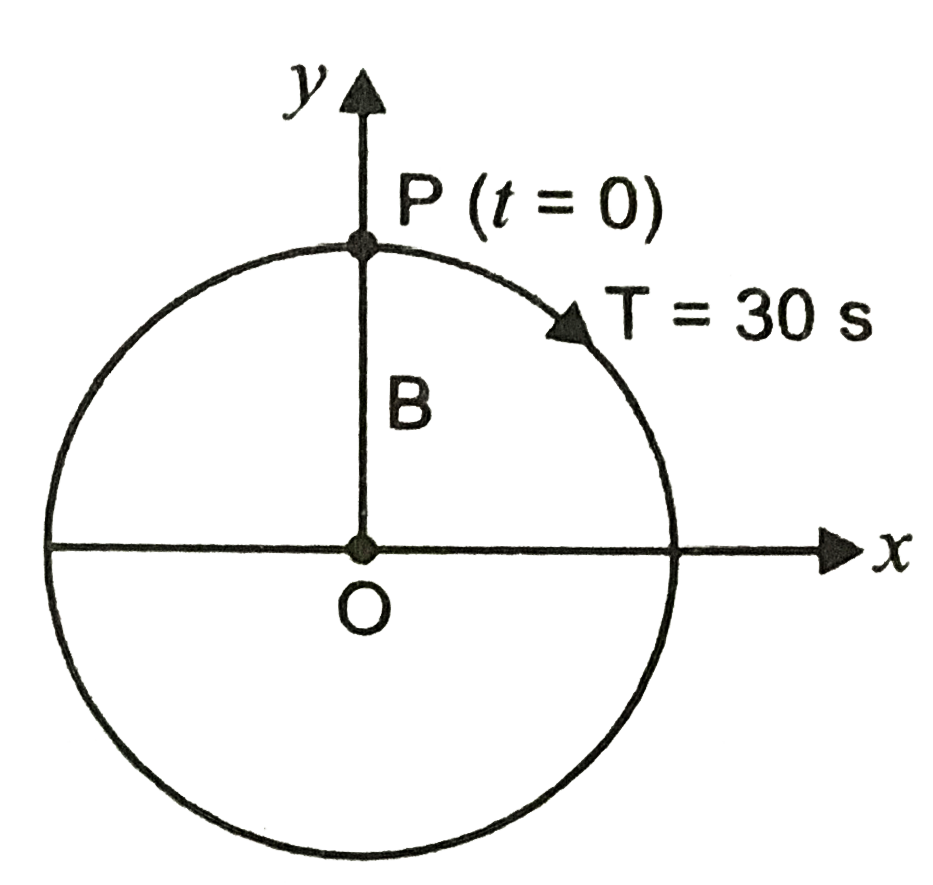
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
View Solution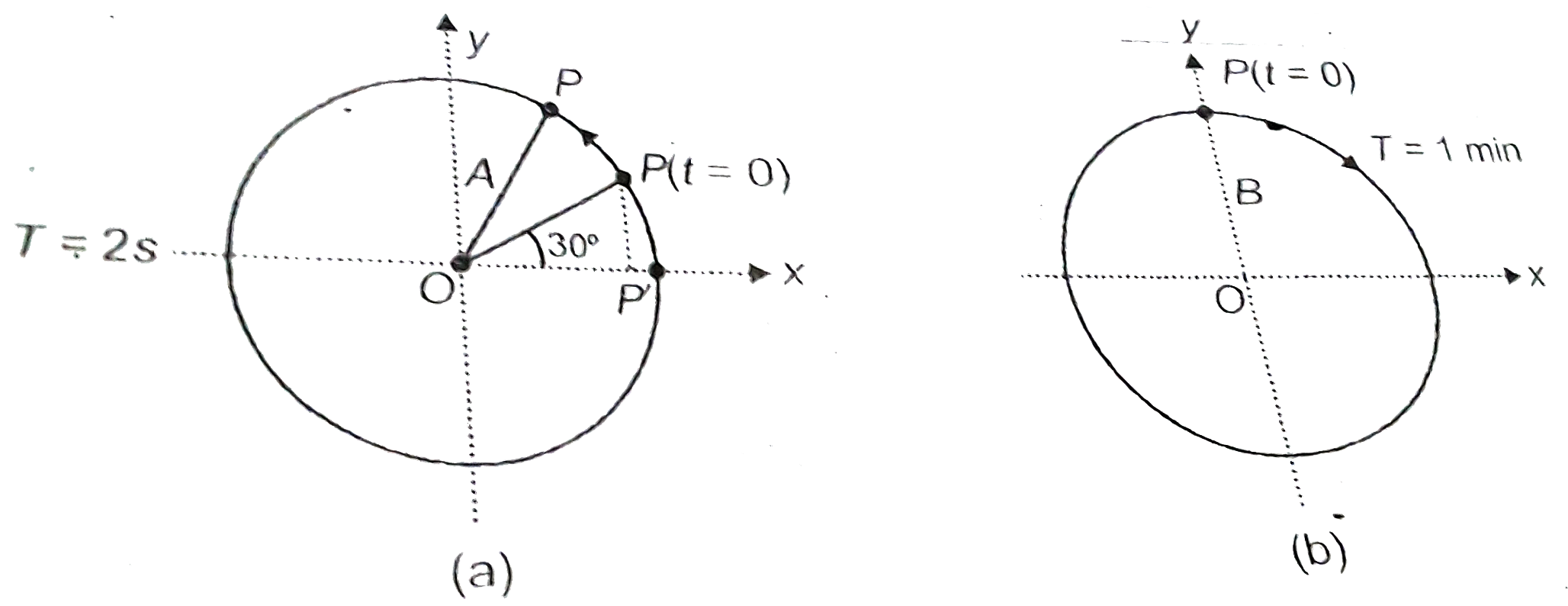
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated in the · figure. The simple harmonic motion of the X-projection of the radius vector of the rotating particle Pis
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P is
View SolutionThe figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated in the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.

View SolutionFigures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
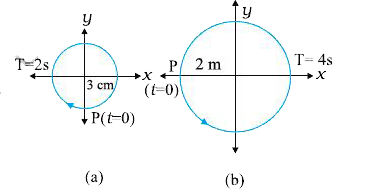
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
View SolutionFigures depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.

View SolutionFigures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
View Solution
