In Young's double slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the centre of the screen is ......Solution in Gujrati
sin−1(λd)
sin−1(λ2d)
sin−1(λ4d)
sin−1(λ3d)
The correct Answer is:C
I=I0cos2{K(r1−r2)2}
I02=I0cos2{2πλ×dsinθ2}
12=cos2{πdsinθλ}
∴1√2=cos{πdsinθλ}
∴π4=πdsinθλ
∴λ4=dsinθ∴θsin−1(λ4d)
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - WAVE OPTICSEXERCISE - SECTION-C NCERT Exemplar Solution (Long Answer Type Questions)5videos
WAVE OPTICS
- BOOK - KUMAR PRAKASHANCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS EXERCISE - Section-D : Multiple Choice Questions (MCQs) (MCQs asked in Competitive Exams)129videos
SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS
Similar Questions
if the intensity of the principal maximum in the single slit Fraunhoffer diffraction pattern, then the intensity when the slit width is double will be .....
03:31View SolutionAt absolute zero temperature Si acts as ……..
01:46View SolutionIn Young's double-slit experiment d/D=10−4 (d = distance between slits, D = distance of screen from the slits) At point P on the screen, resulting intensity is equal to the intensity due to the individual slit I0. Then, the distance of point P from the central maximum is (λ=6000Å)
04:00View SolutionIn a Young's double slit experiment, the separation between the slits is d, distance between the slit and screen is D(Dgtgtd). In the interference pattern, there is a maxima exactly in front for each slit. Then the possible wavelength used in the experiment are:
03:38View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is lambda and I is theintensity of central bright fringe, then intensity at distance from central maximum is
View SolutionIn young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500overset(@)A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. theta on horizontal axis represents the angular position of a point on the screen (a) Find separation d between the slits. (b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
04:20View SolutionIn a Young's double slit experiment, the separation between the slits is d, distance between the slit and screen is D(D>>d). In the interference pattern, there is a maximum exactly in front for each slit. Then the possible wavelength (s) used in the experiment are
07:45View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
01:49View SolutionSeparation between the slits in Young's double-slit experiment is d and screen is placed at a distance D from the slits to observe the interference pattern. Wavelength of light used is lambda . Find the distance of point from centre of screen where intensity falls to (i) half the maximum and (ii) one-fourth of the maximum.
View SolutionIn Young's double-slit experiment , d is separation between the slits. Separation between plane of the slits and screen is D. Wavelength of light used is λ. Number of fringes per unit distance on the screen is
View SolutionIn a Young's double-slit experiment with light of wavelength λ, the separation of slits is d and distance of screen is D such that D>>d>>λ. If the Fringe width is β, the distance from point of maximum intensity to the point where intensity falls to half of maximum intensity on either side is :
07:00View SolutionIn Young's double slit experiment (d)/(D) = 10^(-4) (d = distance between slits, D = distance of screen from the slits) At a point P on the screen the resulting intensity is equal to the intensity due to individual slit I_(0) .Then the distance of point P from the central maximum is (lambda = 6000 Å) :
View SolutionIn the Young's doubel slit experiment, a poiint P on the central bright fringe is such that intensity of point P is 1/4 times the maximum intensity, distance between the slits is d and wavelength λ. Then angular separation of point P is
05:51View SolutionIn Young's Double slit experiment, first maxima is observed at a fixed point P on the screen. Now the screen is continuously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (centre of the screen)
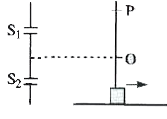 06:13View Solution
06:13View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
04:24View Solution

