A uniform sphere of mass m and radius R is placed on a rough horizontal surface. The spher is struck horizontally at a height h from the floor. Show that the sphere rolls without slipping with a constant velocity, when h=7R/5.
Consider the diagram where a sphere of m and radius ,R, struck horizontally at height h above the floor

the sphere will roll without sipping when ω=vR , where v is linear velocity and ω is angular velocity of the sphere
Now , angular momentum of sphere , about centre of mass
( [We are applying conservation of angular momentum just momentum just before and after struck ]
mv(h−R)=Iω=(25mR2)(vR)
⇒mv(h−R)=25mvR
h−R=25R⇒h=75R Therefore the sphere eill roll without sipping with a constant velocity and hence , no loss of energy ,so (D)→(i)
Torque due to applied force ,F about centre of mass
For τ=0,h=R ,sphere will have only translational motion . it would lose energy by friction
hence , (B)→(iv)
the sphere will spin clokwise when τ>0⇒h>R
therefore , (C)→(ii)
the sphere will spin anti- clockwise when τ<0⇒h<R,(a)→(iii)
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - Long answer type questions
12 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - Long answer type questions
12 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - OSCILLATIONSEXERCISE - All Questions
36 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
Similar Questions

A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,
View SolutionA solid sphere of mass M and radius R is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height h above the surface. The value of h so that the sphere performs pure rolling motion immediately after it has been stuck is

View Solution
Knowledge Check
A uniform sphere of mass m and radius R is placed on a rough horizontal surface [Fig.] The sphere is struck horizontally at a hight h from the floor. Match the following :
(a) h=R/2 (i) Sphere rolls without slipping with a constant velocity and no loss of energy.
(b) h=R (ii) Sphere spins clockwise, loses energy by friction.
(c ) h=3R/2 (iii) Sphere spins anti-clockwise, loses energy by friction.
(d) h=7R/5 (iv) Sphere has only a translational motion, looses energy by friction.
 AA -r, B - s, C - q, D - pBA - s, b - p, C - r, D - qCA - q, B - r, C - p, D - sDA - p, B - q, C - s, D - r
AA -r, B - s, C - q, D - pBA - s, b - p, C - r, D - qCA - q, B - r, C - p, D - sDA - p, B - q, C - s, D - r
A solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.

View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.


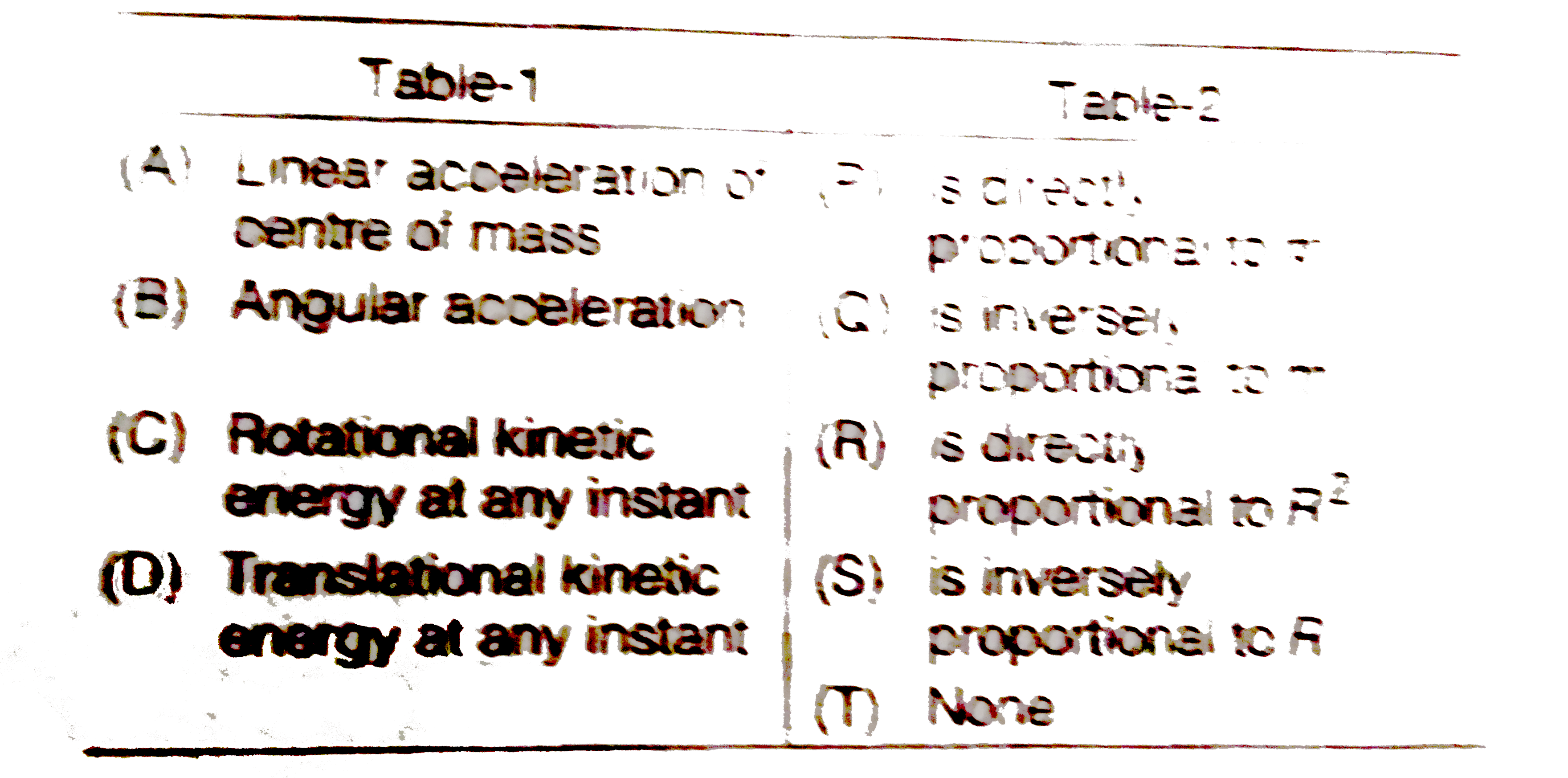
View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View Solution
