A long rod of steel under a tensile stress due to the force acting on the edges along the length. The value of angle 0 for which shearing stress is maximum is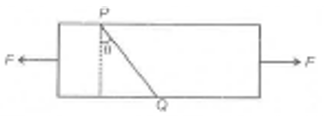 
π4
π3
π6
π2
The correct Answer is:A
Step by step video & image solution for A long rod of steel under a tensile stress due to the force acting on the edges along the length. The value of angle 0 for which shearing stress is maximum is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar
Consider a plane making an angle θ with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.
a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View Solution
Knowledge Check
In the question rumber 66, for what value of θ, shearing stress is maximum?
A0∘B30∘C45∘D90∘A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length. The ratio of tensile stress to the shearing stress on the plane BB' is
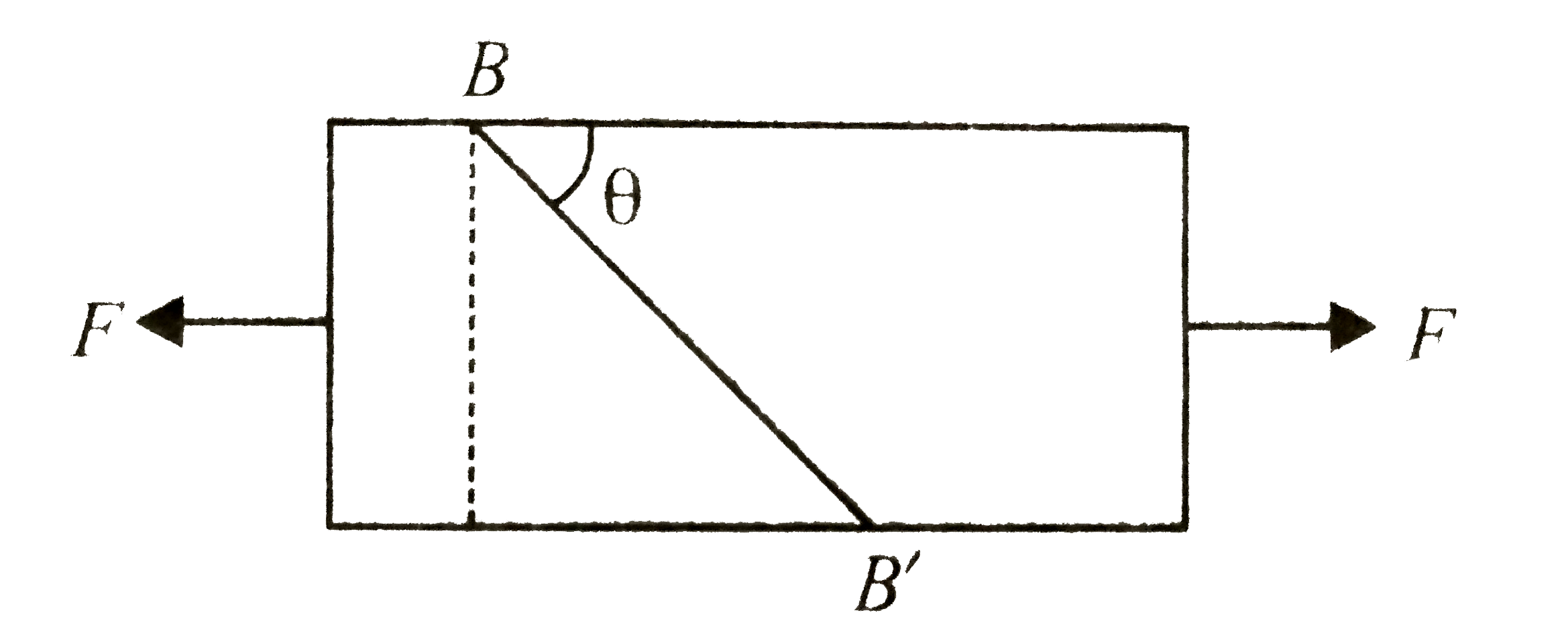AtanθBsecθCcotθDcosθ
A bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
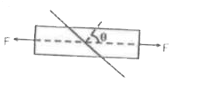
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
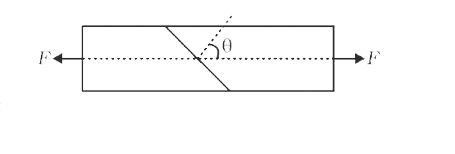
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
View SolutionIn the figure shown a uniform rod of length l and mass m is kept at rest in horizontal position on an elevated edge. The value of x is such that the rod will have maximum angular acceleration α, as soon as it is set free.
View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionWhen a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called strain energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by energy conservation.
In above problem if mass of 10kg falls on the massless collar attached to rod from the height of 99cm then maximum extension in the rod is equal (rod of length 4m, area 4cm2 and young modules 2×1010N/m2 g=10m/sec2)-
View SolutionA uniform rod of mass m and length is acted upon by the forces F1 and F2 Find that:
a. linear-and angular acceleration of the rod.
b. value of x for which the point P does not accelerate.
View Solution