Which of the following options are correct ?
Acceleration due to gravity decrease with icreasing altitude
Acceleration due to gravity increase with increasing depth (assume the earth to be a sphere of uniform density)
Acceleration due to gravity increase with increasing latitude
Acceleration due to gravity is independent of the mass of the earth
The correct Answer is:A, C, D
To solve the question regarding which of the options about acceleration due to gravity are correct, we will analyze each statement step by step.
1. Option 1: Acceleration due to gravity decreases with increasing altitude.
- The formula for acceleration due to gravity at a height H above the Earth's surface is given by:
g′=gR2(R+H)2
- Here, g is the acceleration due to gravity at the surface, R is the radius of the Earth, and H is the height above the surface.
- As H increases, the denominator (R+H)2 increases, which causes g′ to decrease.
- Conclusion: This statement is correct.
2. Option 2: Acceleration due to gravity increases with increasing depth.
- The formula for acceleration due to gravity at a depth d inside the Earth (assuming uniform density) is:
g′=g(1−dR)
- As d increases, the term dR increases, which means g′ decreases.
- Conclusion: This statement is incorrect.
3. Option 3: Acceleration due to gravity increases with increasing latitude.
- The formula for acceleration due to gravity at latitude λ is:
g′=g−ω2Rcos2(λ)
- Here, ω is the angular velocity of the Earth and R is the radius of the Earth.
- As latitude λ increases, cos2(λ) decreases, which means the term ω2Rcos2(λ) decreases, leading to an increase in g′.
- Conclusion: This statement is correct.
4. Option 4: Acceleration due to gravity is independent of the mass of the Earth.
- The formula for acceleration due to gravity is:
g=GMR2
- Here, G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth. This clearly shows that g is directly proportional to the mass of the Earth.
- Conclusion: This statement is incorrect.
Final Answer:
The correct options are 1 and 3.
- The formula for acceleration due to gravity at a height H above the Earth's surface is given by:
g′=gR2(R+H)2
- Here, g is the acceleration due to gravity at the surface, R is the radius of the Earth, and H is the height above the surface.
- As H increases, the denominator (R+H)2 increases, which causes g′ to decrease.
- Conclusion: This statement is correct.
- The formula for acceleration due to gravity at a depth d inside the Earth (assuming uniform density) is:
g′=g(1−dR)
- As d increases, the term dR increases, which means g′ decreases.
- Conclusion: This statement is incorrect.
- The formula for acceleration due to gravity at latitude λ is:
g′=g−ω2Rcos2(λ)
- Here, ω is the angular velocity of the Earth and R is the radius of the Earth.
- As latitude λ increases, cos2(λ) decreases, which means the term ω2Rcos2(λ) decreases, leading to an increase in g′.
- Conclusion: This statement is correct.
- The formula for acceleration due to gravity is:
g=GMR2
- Here, G is the gravitational constant, M is the mass of the Earth, and R is the radius of the Earth. This clearly shows that g is directly proportional to the mass of the Earth.
- Conclusion: This statement is incorrect.
The correct options are 1 and 3.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - Very short Answer type question11videos
GRAVITATION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - Short Answer type question6videos
GRAVITATION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)31videos
KINETIC THEORY
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following options is correct ?
AStenothermal organismEurythermal organismFrogLizardBStenothermal organismEurythermal organismFrogManCStenothermal organismEurythermal organismManLizardDStenothermal organismEurythermal organismPolar bearCoconut tree - Question 2 - Select One
Which of the following options is correct ?
AStenothermal organismEurythermal organismFrogLizardBStenothermal organismEurythermal organismFrogManCStenothermal organismEurythermal organismManLizardDStenothermal organismEurythermal organismPolar bearCoconut tree - Question 3 - Select One
Which of the following options is correct ?
AStenothermal organismEurythermal organismFrogLizardBStenothermal organismEurythermal organismFrogManCStenothermal organismEurythermal organismManLizardDStenothermal organismEurythermal organismPolar bearCoconut tree
Which of the following options is correct?
View SolutionWhich are the following options are correct
1. Heroin-Stimulant
2. Marijuana-Cardiovascular
3. Cocaine-Hallucination
4. Morphine-SedativeView SolutionIf graph of y= f(x) is as shown in figure, then which of the following options is/are correct?
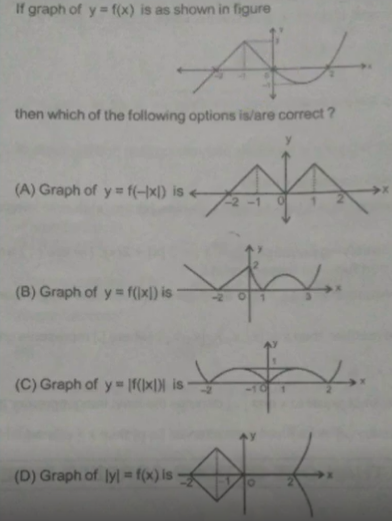 View Solution
View SolutionA uniform rod of length l is applied upon by two forces at its either end as shown. Surface is smooth. Which of the following option is correct ?
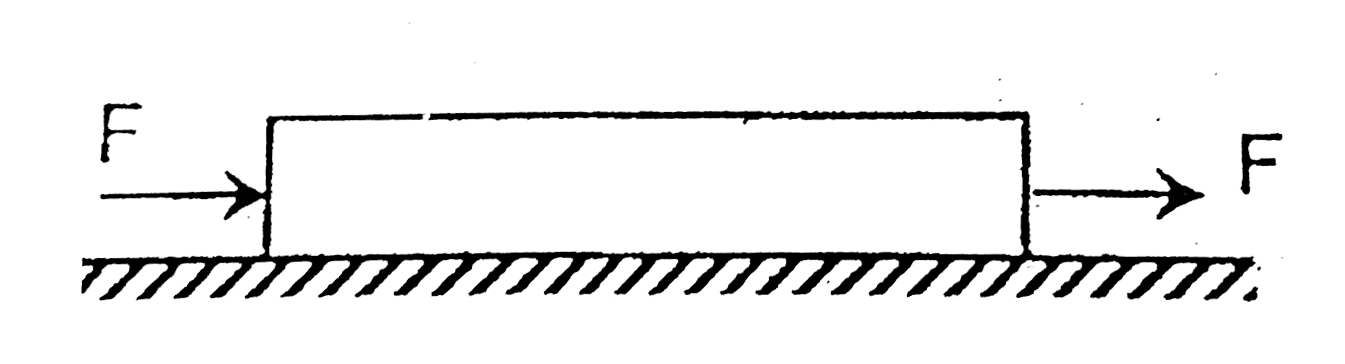 View Solution
View SolutionTwo conductors of equal volumes having non-uniform cross-section are joined as show in figure. The number density of free electrons is more in conductor 2. As current passes through the system. Which of the following option is correct ?
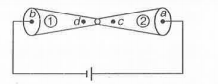 View Solution
View Solution


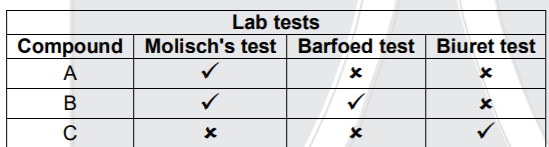 Which of the following options is correct ?
Which of the following options is correct ?