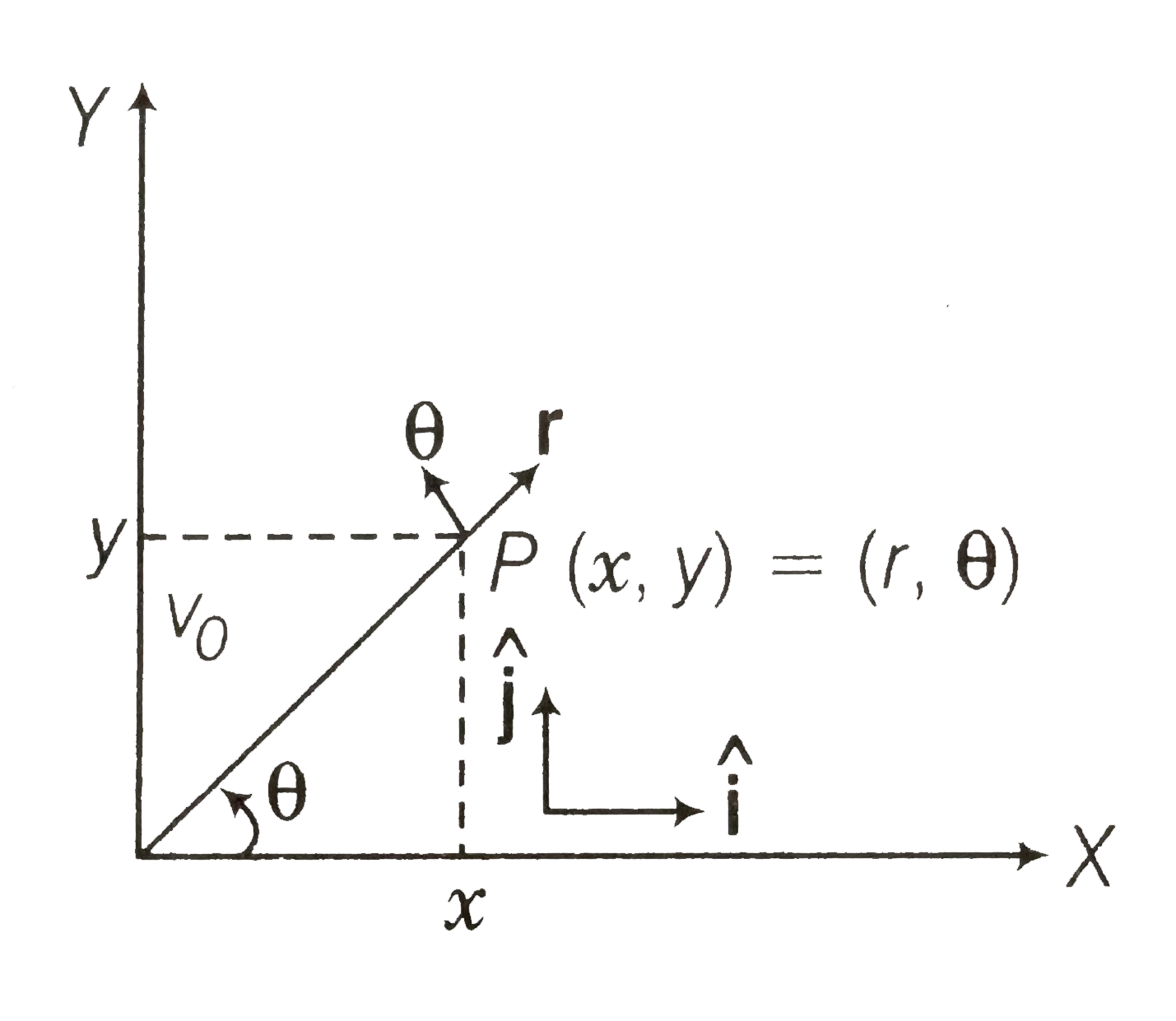
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates $A = A_{x} ˆ i + A_{y} ˆ j$ , where $ˆ i$ and $ˆ j$ are unit vector along x and y-directions, respectively and $A_{x}$ and $A_{y}$ are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as $A = A_{r} ˆ r + A_{θ} ˆ θ$ , where $ˆ r = \frac{r}{r} = cos θ ˆ i + sin θ ˆ j$ and $ˆ θ = - sin θ ˆ i + cos θ ˆ j$ are unit vectors along direction in which r and $θ$ are increasing.
(a) Express $ˆ i$ and $ˆ j$ in terms of $ˆ r$ and $ˆ θ$ .
(b) Show that both $ˆ r$ and $ˆ θ$ are unit vectors and are perpendicular to each other.
(c) Show that $\frac{d}{d t} (ˆ r) = ω ˆ θ$ , where $ω = \frac{d θ}{d t}$ and $\frac{d}{d t} (ˆ θ) = - θ ˆ r$ .
(d) For a particle moving along a spiral given by $r = a θ ˆ r$ , where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.

Text Solution

Verified by Experts

(a) Given, unit vector $ˆ r = cos θ ˆ i + sin θ ˆ j ... (i)$
$ˆ θ = - sin θ ˆ i + cos θ ˆ j ... (i i)$
Multiplying Eq. (i) by $sin θ$ and Eq. (ii) with $cos θ$ and adding
$ˆ r sin θ + ˆ θ cos θ = sin θ . cos θ ˆ i + {sin}^{2} θ (j) + {cos}^{2} θ ˆ j - sin θ . cos θ ˆ i$
$= ˆ j ({cos}^{2} θ + {sin}^{2} θ) = ˆ i$
$\Rightarrow ˆ r sin θ + ˆ θ cos θ = ˆ j$
By Eq. $(i) \times cos θ - Eq. (i i) \times sin θ$
$n (ˆ r cos t h e t a - ˆ θ sin θ) = ˆ i$
(b) $ˆ r . ˆ θ = (cos θ ˆ i + sin θ ˆ j) . (- sin θ ˆ i + cos θ ˆ j) = - cos θ . sin θ + sin θ . cos θ = 0$
$\Rightarrow θ = 90^{\circ}$ Angle between $ˆ r$ and $ˆ θ$ .
(c) Given, $ˆ r = cos θ ˆ i + sin θ ˆ j$
$\frac{d ˆ r}{d t} = \frac{d}{d t} (cos θ ˆ i + sin θ ˆ j) = - sin θ . \frac{d θ}{d t} ˆ i + cos θ . \frac{d θ}{d t} ˆ j$
$= ω [- sin θ ˆ i + cos θ ˆ j] [∵ θ = \frac{d θ}{d t}]$
(d) Given , $r = a θ ˆ r$ , here, writing dimensions $[r] = [a] [θ] [ˆ r]$
$\Rightarrow L = [a] % 1 \Rightarrow [a] = L = [M^{0} L^{1} T^{0}]$
(e) Given, a = 1 unit $r = θ ˆ r = θ [cos θ ˆ i + sin θ ˆ j]$
Velocity, $v = \frac{d r}{d t} = \frac{d θ}{d t} ˆ r + θ \frac{d}{d t} ˆ r = \frac{d θ}{d t} ˆ r + θ \frac{d}{d t} [cos θ ˆ i + sin θ ˆ j]$
$= \frac{d θ}{d t} ˆ r + θ [(- sin θ ˆ i + cos θ ˆ j) \frac{d θ}{d t}]$
$= \frac{d θ}{d t} ˆ r + θ ˆ θ ω = ω ˆ r + ω θ ˆ θ$
Acceleration, $a = \frac{d}{d t} [ω ˆ r + ω θ ˆ θ] = \frac{d}{d t} [\frac{d θ}{d t} ˆ r + \frac{d θ}{d t} (θ ˆ θ)]$
$= \frac{d^{2} θ}{{d t}^{2}} ˆ r + \frac{d θ}{d t} . \frac{d ˆ r}{d t} + \frac{d^{2} θ}{{d t}^{2}} θ ˆ θ + \frac{d θ}{d t} \frac{d}{d t} (θ ˆ θ)$
$= \frac{d^{2} θ}{{d t}^{2}} ˆ r + ω [- sin θ ˆ i + sin θ ˆ j] + \frac{d^{2} θ}{{d t}^{2}} θ ˆ θ + \frac{ω d}{d t} (θ ˆ θ)$
$= \frac{d^{2} θ}{{d t}^{2}} ˆ r + ω^{2} ˆ θ + \frac{d^{2} θ}{{d t}^{2}} \times θ ˆ θ + ω^{2} ˆ θ + ω^{2} θ (- ˆ r)$
$(\frac{d^{2} θ}{d t v^{2}} - ω^{2}) ˆ r + (2 ω^{2} + \frac{d^{2} θ}{{d t}^{2}} θ) θ$

Updated on:21/07/2023

The angle which the vector $\to A = 2 ˆ i + 3 ˆ j$ makes with the y-axis, where $ˆ i$ and $ˆ j$ are unit vectors along x- and y-axis, respectively, is
A ${cos}^{- 1} (3 / 5)$
B ${cos}^{- 1} (2 / 3)$
Ctan^(-1)(2//3)
D ${sin}^{- 1} (2 / 3)$
The angle $θ$ between the vector $\to p = ˆ i + ˆ j + ˆ k$ and unit vector along X-axis is
A ${cos}^{- 1} (\frac{1}{\sqrt{3}})$
B ${cos}^{- 1} (\frac{1}{\sqrt{2}})$
C ${cos}^{- 1} (\frac{\sqrt{3}}{2})$
D ${cos}^{- 1} (\frac{1}{2})$
If $ˆ i, ˆ j and ˆ k$ are unit vectors along x,y and z-axis respectively, the angle $θ$ between the vector $ˆ i + ˆ j + ˆ k and vector ˆ j$ is given by
A $θ = {cos}^{- 1} (\frac{1}{\sqrt{3}})$
B $θ = {sin}^{- 1} (\frac{1}{\sqrt{3}})$
C $θ = {cos}^{- 1} (\frac{\sqrt{3}}{2})$
D $θ = {sin}^{- 1} (\frac{\sqrt{3}}{2})$