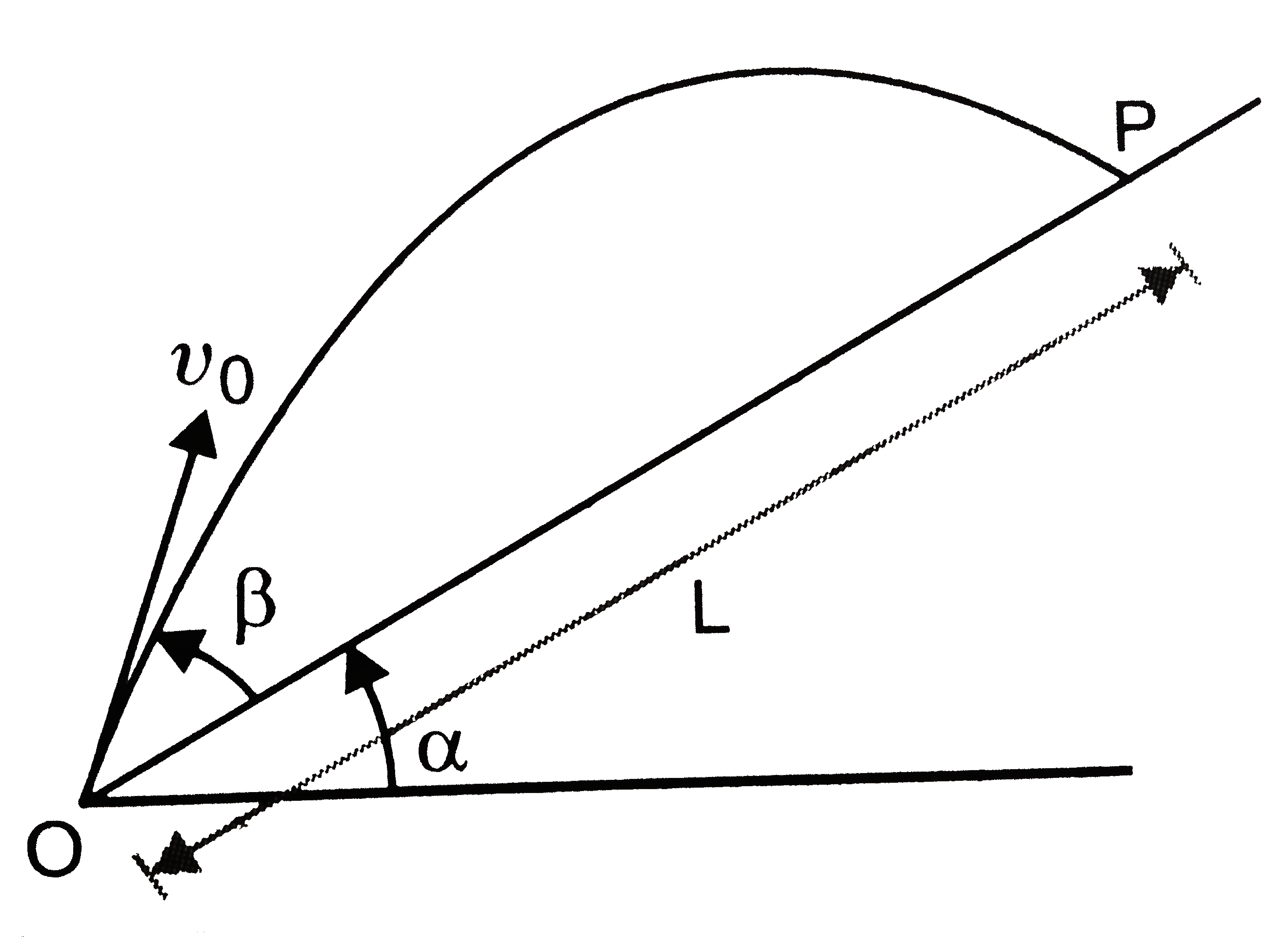
A particle is projected in air at an angle $β$ to a surface which itself is inclined at an angle $α$ to the horizontal (Fig. 2 (EP). 26)
(a) Find an expression for range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface). (b) Time of flight. 9c ) $β$ at which range will be maximum.

Video Solution

Text Solution

Verified by Experts

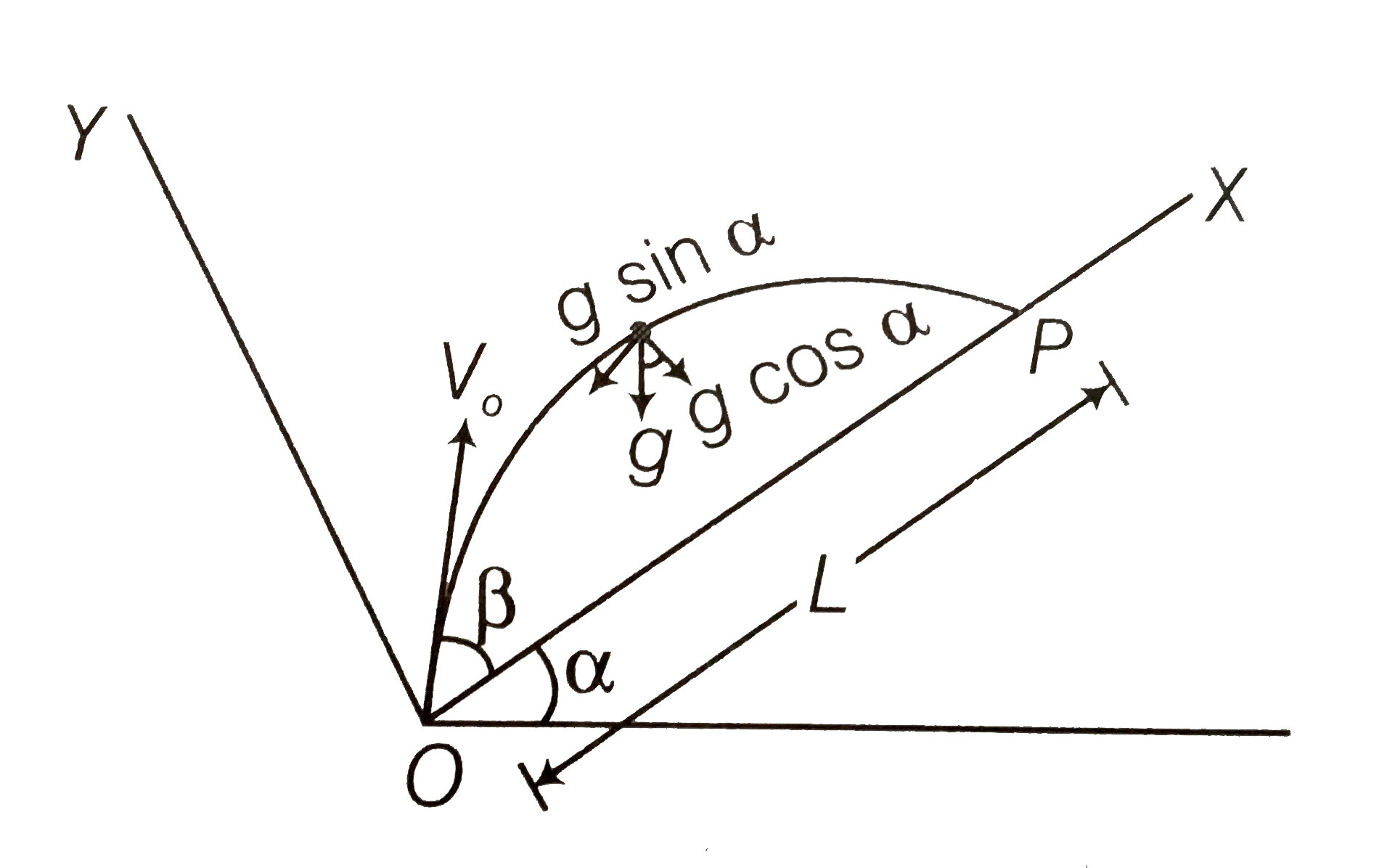
Consider the adjacent diagram.
Mutually perpendicular x and y-axes are shown in the diagram.
Particle is projected from the point O.
Let time taken in reaching from point O to point P is T.
(b) Considering motion along vertical upward direction perpendicular to OX.
For the journey O to P.
$y = 0, u_{y} = v_{0} sin β, a_{y} = - g cos α, t = T$
Applying equation,
$y = u_{y} t + \frac{1}{2} a_{y} t^{2}$
$\Rightarrow 0 = v_{0} sin β T + \frac{1}{2} (- g cos α) T^{2}$
$\Rightarrow T [v_{0} sin β - \frac{g cos α}{2} T] = 0$
$\Rightarrow T = 0, T = \frac{2 v_{0} sin β}{g cos α}$
As T = 0, corresponding to point O
Hence, $T = Time of flight = \frac{2 v_{0} sin β}{g cos α}$
(a) Considering motion along OX,
$x = L, u_{x} = v_{0} cos β, a_{x} = - g sin α$
$t = T = \frac{2 v_{0} sin β}{g cos α}$
$x = u_{x} t + \frac{1}{2} a_{x} t^{2}$
$\Rightarrow L = v_{0} cos β T + \frac{1}{2} (- g sin α) T^{2}$
$\Rightarrow L = v_{0} cos β T - \frac{1}{2} g sin α T^{2}$
$= T [v_{0} cos β - \frac{1}{2} g sin α T]$
$= T [v_{0} cos β - \frac{1}{2} g sin α \times \frac{2 v_{0} sin β}{g cos α}]$
$= \frac{2 v_{0} sin β}{g cos α} [v_{0} cos β - \frac{v_{0} sin α sin β}{g cos α}]$
$= \frac{2 v_{0}^{2} sin β}{g {cos}^{2} α} [cos β . cos α - sin α . sin β]$
$\Rightarrow L = \frac{2 v_{0}^{2} sin β}{g {cos}^{2} α} cos (α + β)$
(c) For range (L) to be maximum.
Let, $Z = sin β . cos (α + β)$
$= sin β [cos α . cos β - sin α . sin β]$
$= \frac{1}{2} [cos α . sin 2 β - 2 sin α . {sin}^{2} β]$
$= \frac{1}{2} [sin 2 β . cos α - sin α (1 - cos 2 β)]$
$\Rightarrow z = \frac{1}{2} [sin 2 β . cos α - sin α + sin α . cos 2 β]$
$= \frac{1}{2} [sin 2 β . cos α + cos 2 β . sin α - sin α]$
$= \frac{1}{2} [sin (2 β + α) - sin α]$
For z to be maximum,
$sin (2 = β + α)$ =maximum = 1
$\Rightarrow 2 β + α = \frac{π}{2} or, β = \frac{π}{4} - \frac{α}{2}$

Updated on:21/07/2023

|

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-MOTION IN A PLANE-Multiple Choice Questions

Home
Ask Doubt
Profile