Sample of two radioactive nuclides A and B are taken. λA and λB are the disintergration constants of A and B respectively. In which of the following cases, the two sample can simultaneously have the same decay rate at any time ?
initial rate of decay of A is twice the initial rate of decay of B and λA=λB
initial rate of decay of A is twice the initial rate of decay of B and λA>λB
Initial rate of decay of B is twice the initial rate of decay of A and λA>λB
Initial rate of decay of B is same as the rate of decay of A at t =2h and λB<λA
The correct Answer is:b,d
To determine when two radioactive nuclides A and B can simultaneously have the same decay rate at any time, we need to analyze the relationship between their decay rates and disintegration constants.
1. Understanding Decay Rate:
The decay rate (activity) of a radioactive sample is given by the formula:
R=λN
where R is the decay rate, λ is the disintegration constant, and N is the number of undecayed nuclei at a given time.
2. Setting Up the Condition:
For nuclides A and B to have the same decay rate at any time, we can set their decay rates equal to each other:
RA=RB
This implies:
λANA=λBNB
3. Analyzing the Relationship:
Rearranging the equation gives:
NANB=λBλA
This means that the ratio of the number of undecayed nuclei of A to that of B must equal the ratio of their disintegration constants.
4. Considering Initial Conditions:
If we consider the initial conditions where NA and NB are the initial amounts of A and B respectively, we can express the relationship at t=0:
NA(0)=NA0,NB(0)=NB0
Therefore, at t=0:
λANA0=λBNB0
5. Conclusion:
For the two samples A and B to have the same decay rate at any time, the ratio of their initial amounts must be inversely proportional to their disintegration constants. Thus, if the initial amount of A is twice that of B, and the disintegration constant of A is greater than that of B, they can have the same decay rate.
Final Answer:
The two samples A and B can simultaneously have the same decay rate at any time if:
- The initial amount of A is appropriately related to the initial amount of B based on their disintegration constants.
The decay rate (activity) of a radioactive sample is given by the formula:
R=λN
where R is the decay rate, λ is the disintegration constant, and N is the number of undecayed nuclei at a given time.
For nuclides A and B to have the same decay rate at any time, we can set their decay rates equal to each other:
RA=RB
This implies:
λANA=λBNB
Rearranging the equation gives:
NANB=λBλA
This means that the ratio of the number of undecayed nuclei of A to that of B must equal the ratio of their disintegration constants.
If we consider the initial conditions where NA and NB are the initial amounts of A and B respectively, we can express the relationship at t=0:
NA(0)=NA0,NB(0)=NB0
Therefore, at t=0:
λANA0=λBNB0
For the two samples A and B to have the same decay rate at any time, the ratio of their initial amounts must be inversely proportional to their disintegration constants. Thus, if the initial amount of A is twice that of B, and the disintegration constant of A is greater than that of B, they can have the same decay rate.
The two samples A and B can simultaneously have the same decay rate at any time if:
- The initial amount of A is appropriately related to the initial amount of B based on their disintegration constants.
Topper's Solved these Questions
Similar Questions
Two radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
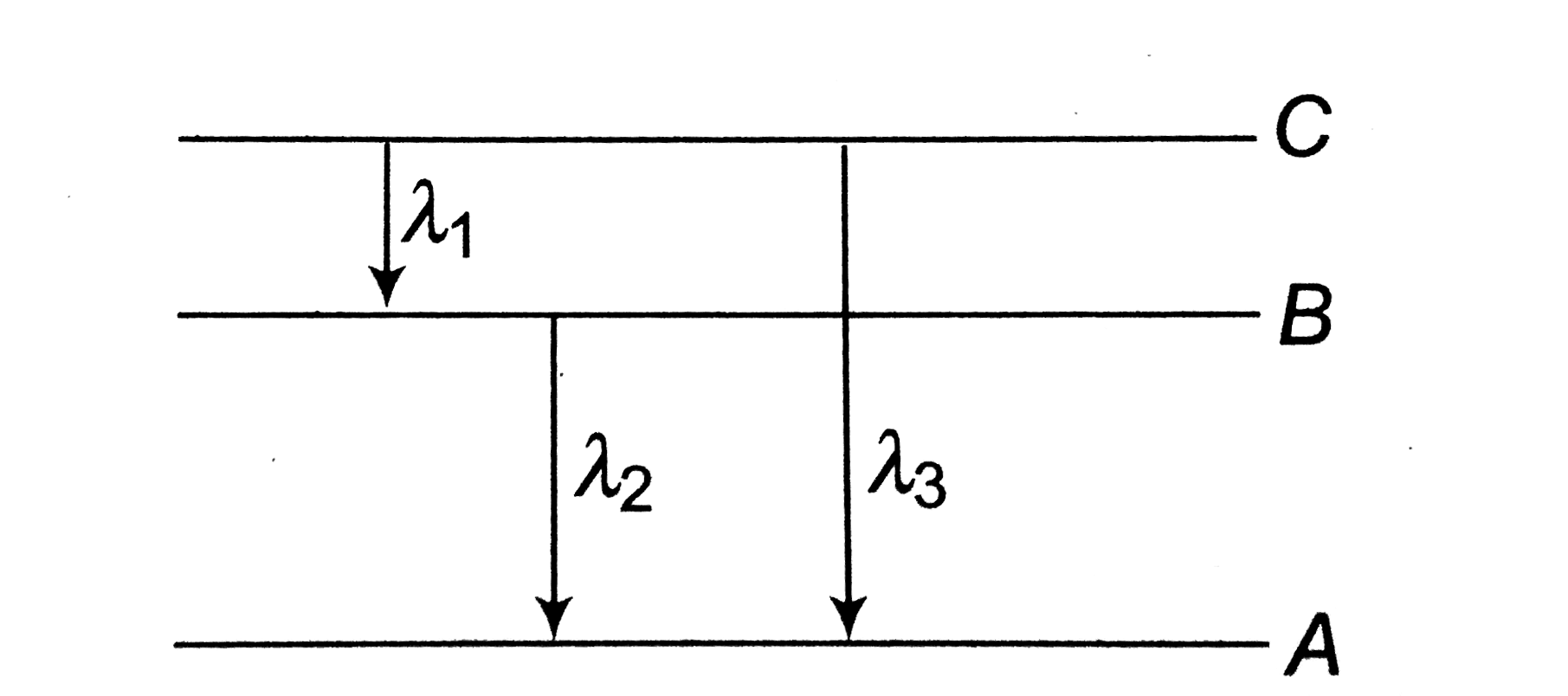
View SolutionEnergy levels A,B,C of a certain atoms corresponding to increasing values of energy level i.e., EA<EB<EC. If λ1,λ2 and λ3 are the wavelengths of radiations corresponding to the transitions C to B,B to A and C to A respectively which of the following statement is correct?
View Solution
Knowledge Check
- Question 1 - Select One
Energy levels A,B,C of a certain atom corresponding to increasing values of energy i.e., EA<EB<EC. If λ1,λ2,λ3 are the wavelengths of radiations correspnding to the transitions C to B,B to A and C to A respectively, which of the following statements is correct?
 Aλ3=λ1+λ2Bλ1+λ2+λ3=0Cλ23=λ21+λ22Dλ=λ1λ2λ1+λ2
Aλ3=λ1+λ2Bλ1+λ2+λ3=0Cλ23=λ21+λ22Dλ=λ1λ2λ1+λ2 - Question 2 - Select One
Two redioactive nuclei A and B have disintegration constants λAandλB and initially NAandNB number of nuclei of them are taken, then the time after which their undisintegrated nuclei are same is
AλAλB(λA−λB)In(NBNA)B1(λA+λB)In(NBNA)C1(λB−λA)In(NBNA)D1(λA−λB)In(NBNA)
Energy levels A,B,C of a certain atom corresponding to increasing values of energy i.e., EA<EB<EC. If λ1,λ2,λ3 are the wavelengths of radiations correspnding to the transitions C to B,B to A and C to A respectively, which o fthe following statements is correct?
 View Solution
View SolutionTwo radioactive nuclei A and B are taken with their disintegration constant λA and λB and initially NA and NB number of nuclei are taken then the time after which their undisintegrated nuclei are same is
View SolutionA stable nuclei C is formed from two radioactive nuclei A and B with decay constant of λ1 and λ2 respectively. Initially, the number of nuclei of A is N0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.
View SolutionThe decay constant of a radioactive substance for a and β emission are λa and λβ respectively. It the substance emits a and β simultaneously, the average half life of the material will be_______
View SolutionThe energies of energy levels A, B and C for a given atom are in the sequence EA<EB<EC. If the radiations of wavelength λ1,λ2 and λ3 are emitted due to the atomic transitions C to B, B to A and C to A respectively then which of the following relations is correct :-
View SolutionThe threshold wavelength for two photosensitive surfaces A and B are λ1 and λ2 respectively. What is the ratio of the work functions of the two surfaces?
View Solution

